0 Circle Apollóniusz
0.6. Apollonius kör
Tekintsük a probléma megtalálni a pontok helye a síkban, az arány a távolság, amely a két adatpont - állandó. A probléma megoldására használjuk a módszert a koordináták, nevezetesen megkapjuk az egyenletet formák által alkotott lókusz, majd tanulmányozza geometriai tulajdonságai.
Bemutatunk egy derékszögű koordináta-rendszert, adja meg, mint a kezdete az egyik adott két pont A és B (például B) és az Ox tengely - úgy, hogy a második pont (legyen ez a pont) fekvő pozitív fele (lásd 10.6 ábra .. .1).
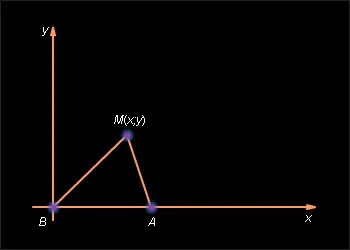
Ebben a koordinátarendszerben, a B pont koordinátái (0, 0), és az A pont - (a; 0), ahol a> 0. Legyen M (x y.) - tetszőleges pont az említett feltételeket kielégítő a probléma, azaz AM = k · BM. ahol k - adott pozitív szám. Ha k = 1, ez azt jelenti, hogy a kívánt készlet áll pontok egyenlő távolságra az adatokat A és B pontok a tulajdonságait a merőleges a szegmens, ebből következik, hogy a kívánt beállított ebben az esetben egy egyenes vonal áthalad a közepén merőleges az AB szakasz OX tengelyen. Most k ≠ 1. tétel 10,2 mi van, és az állapota az M pont látja el a kívánt beállítási felírható
Ez az egyenlet ekvivalens az egyenletek
Kiszemelésével tökéletes négyzet, megkapjuk
Ez az egyenlet a kör közepén a ponton fekvő tengely OX. és a sugár
Az így kapott kört nevezték az ókori görög földmérő Apollonius. úgy döntött, hogy megbízzák egy tisztán geometriai módszer.
oldal 1
0 Circle Apollóniusz
16.36kb. 1 p.
Ellipszis eszköz, és tartsa lenyomva a Ctrl billentyűt, rajzol két kört, amelyek közül az egyik átmérője valamivel nagyobb, mint az utóbbi. Kisebb körben töltjük az eszköz használata Fointain Fill
15.18kb. 1 p.