11 szeminárium
Curves másodrendű a síkban.
háttér
I. A vonal egyenlete a gépen.
Opredelenie.Uravneniem vonal (görbe) a síkban
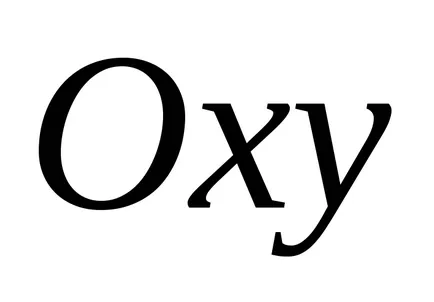

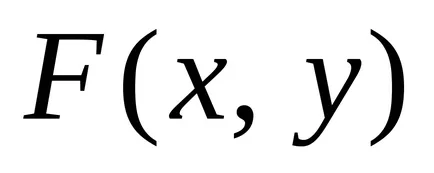


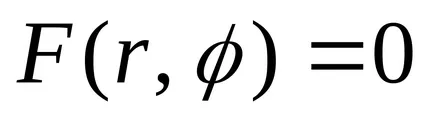
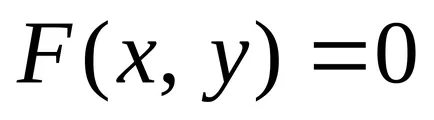

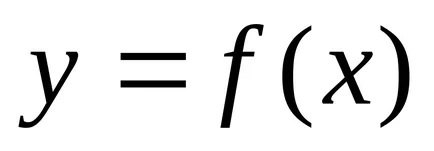
Mivel a egy pont koordinátáit a vonal csatlakozik a következő egyenlet által, a vonal egydimenziós mértani objektum. A probléma megtalálni a metszéspontja a két vonal által megadott egyenletek

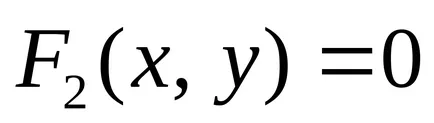
csökken megoldása egy rendszer két egyenlet két ismeretlent:
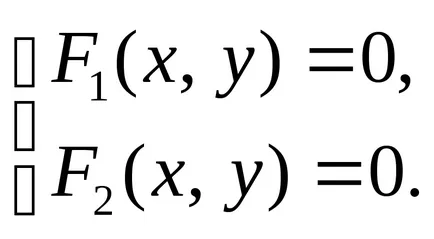
Vonal a gépen is megadható parametrikus két egyenlet
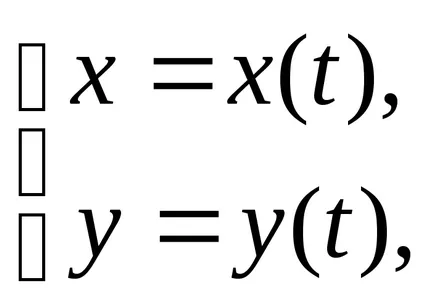
ahol
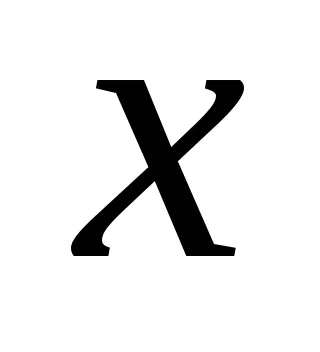

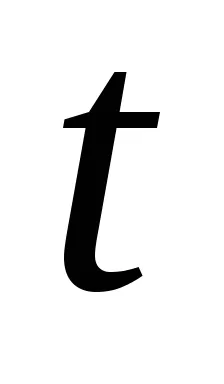
Íme néhány példa a vonalak.
A kör sugara
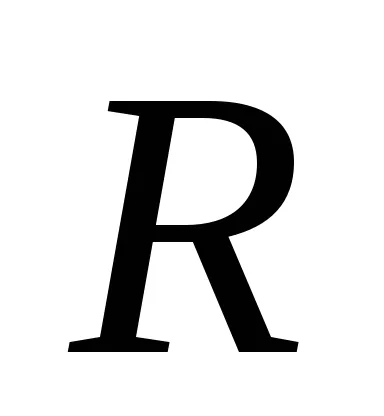
Egyenleteket, mint egy kör alakú:
a)
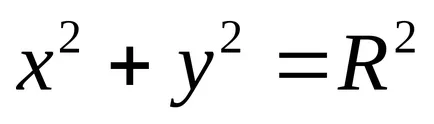
b)
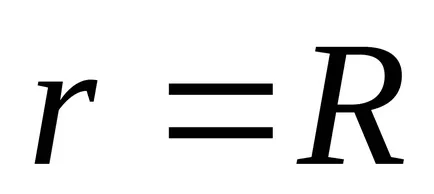
c)

A paraméteres formában a ciklois egyenletnek formájában
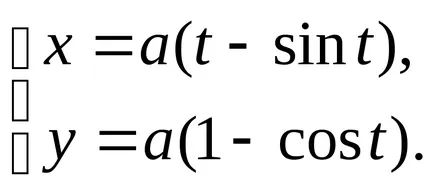
Leírja a görbe pont a körön

Astroid által megadott egyenletek:
a)
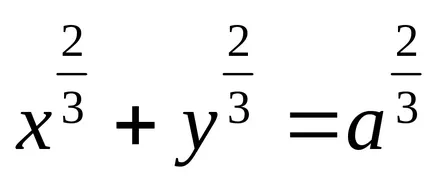
b)
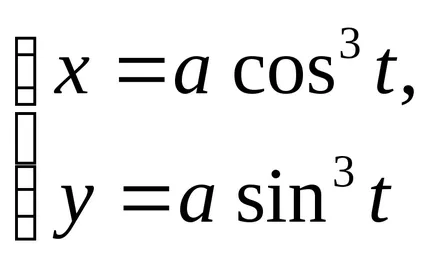
Leírja a görbe pont a körön
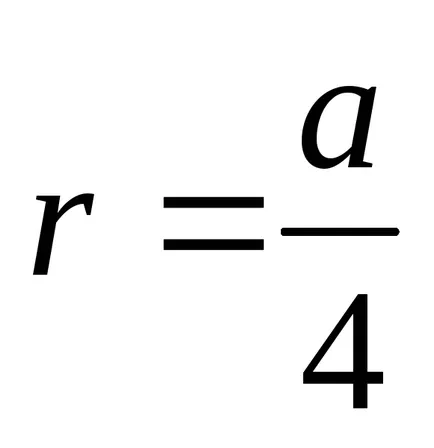
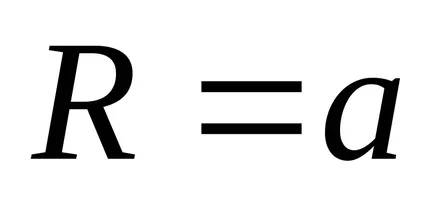
Egyenlet kardioid polár koordinátarendszerben megadott
.
Ez a görbe írja le a körön pont
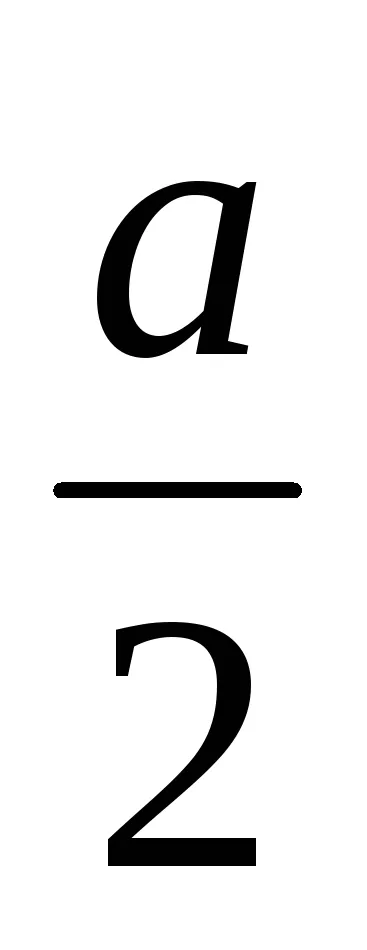
Kardioid egyenlet egy speciális esete (
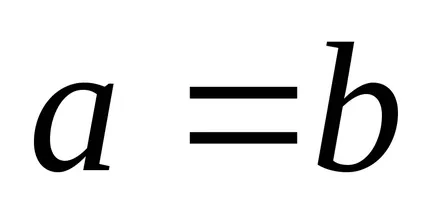
.
Bernoulli lemniscate által megadott egyenletek:
a) - a Descartes-féle koordináta-rendszerben;
b)
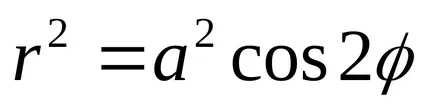
A terméket a távolságok az egyes pont mozgató Bernoulli két adatpont
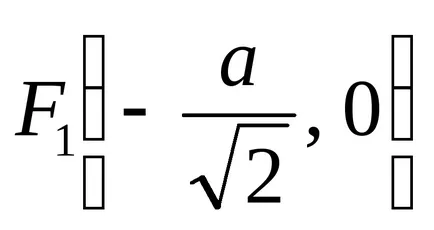
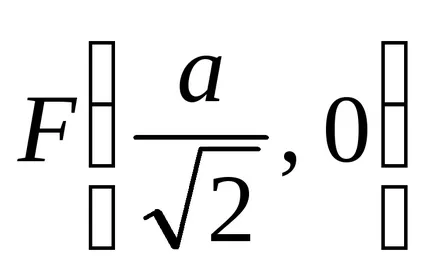


Derékszögű lap által adott egyenletek:
a) - a Descartes-féle koordináta-rendszerben;
b)
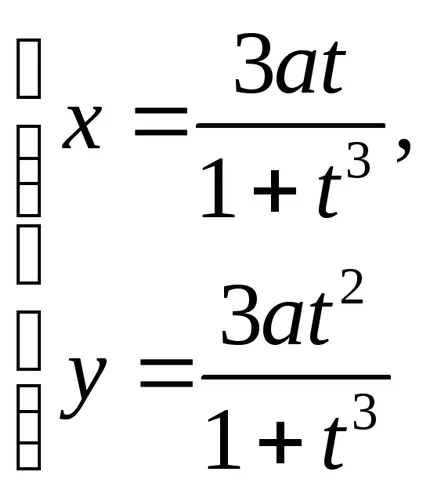
A paraméteres formában a görbe által megadott egyenletek
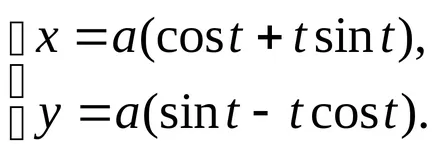
9) emelkedett háromszorosára.
ez a görbe a polár koordinátarendszerben egyenlet által definiált
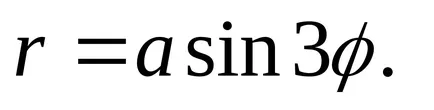
10) chetyrehlepestkovaya emelkedett.
A egyenletnek formájában
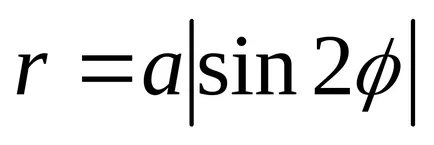
11) egy spirális Archimedes.
Ez a görbe a polár koordinátarendszerben által leírt egyenlet
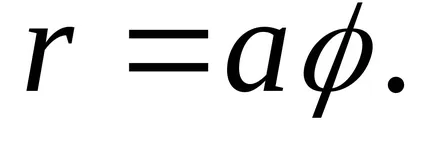
12) egy logaritmikus spirál.
A egyenletnek formájában
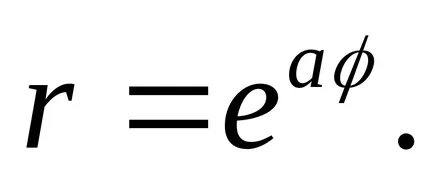
13) hiperbolikus spirál.
Ez a görbe adja meg egyenletek
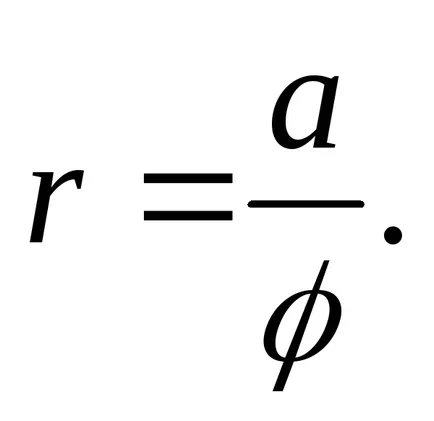
II. Az általános egyenlete másodrendű és hozza kanonikus formában.
Az általános másodfokú egyenlet a vonal formájában
Feltételezzük, hogy
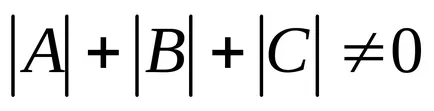
Párhuzamos fordítás származására.
Új (alapozás) koordináta rendszerben bevezetett segítségével kapcsolatok

Az új koordináta rendszerben az (1) egyenlet válik
Figyelembe állandóként
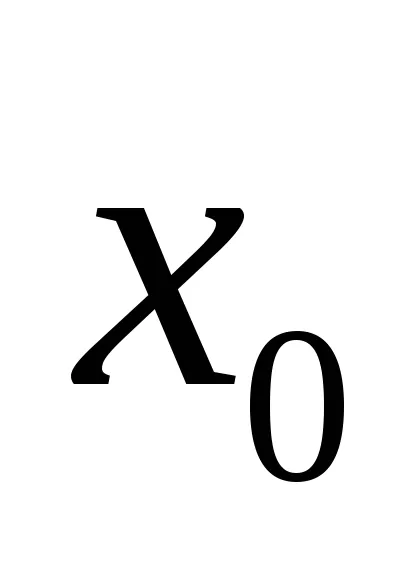
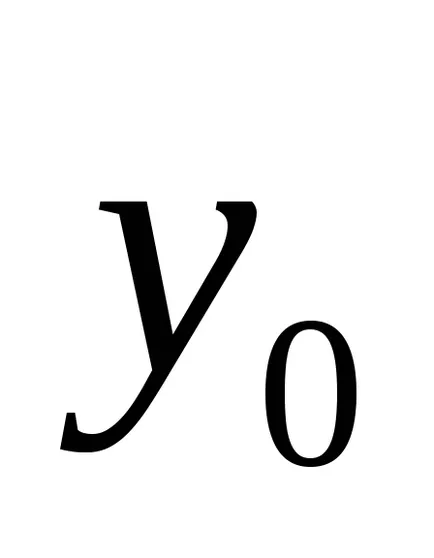
ki tudjuk küszöbölni a görbék egyenlete a feltételeket az első fokú változók
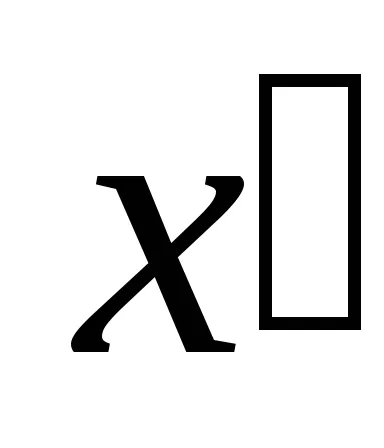


Megoldásában az egyenletrendszert (2) eset lehetséges:
1)
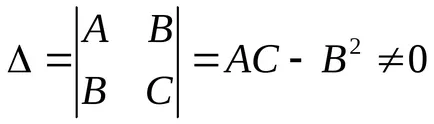
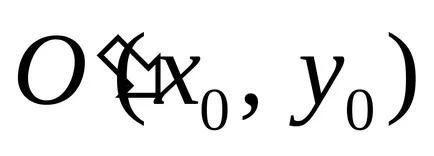
2). Lehetnek olyan esetek:
a) az egyenletrendszert nincs megoldás, a görbék nem a központ és az úgynevezett parabola;
b) az egyenletrendszert van végtelen számú megoldást, a görbe az úgynevezett degenerált parabola (vagy egy pár képzeletbeli párhuzamos vonalak egy pont).
Ezután vegyük azt az esetet központi részletei görbék. Azt, hogy a forgatás a Koordinátatengelyek szög

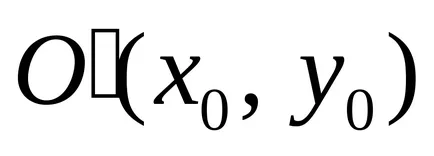
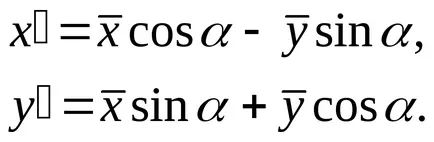
görbéje (3) egyenlet válik
,
Mi választjuk ki a forgásszög a Koordinátatengelyek

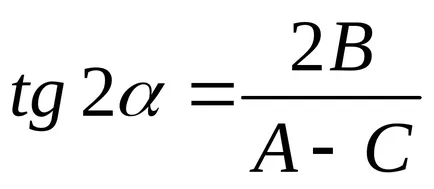
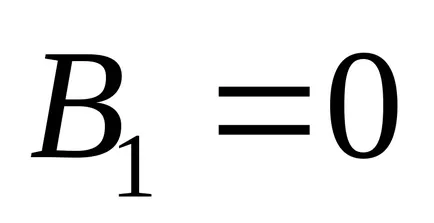
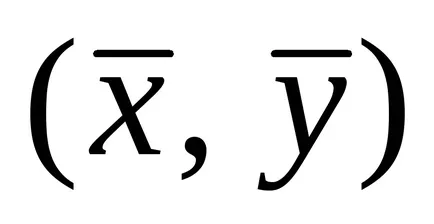
.
Példa. Hagyja, hogy a kanonikus egyenlete másodrendű görbe, amelyre. Találunk a koordinátákat a központ a görbe az egyenletrendszert


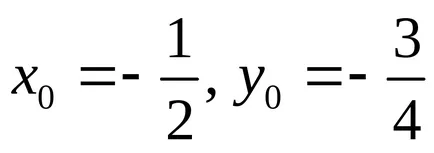
.
Megjegyezzük, hogy az adott, azaz görbe A görbe ellipszis. Forgassuk el a koordináta-tengelyek szögben

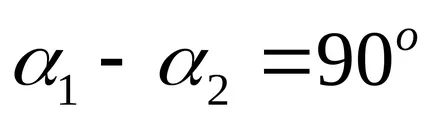
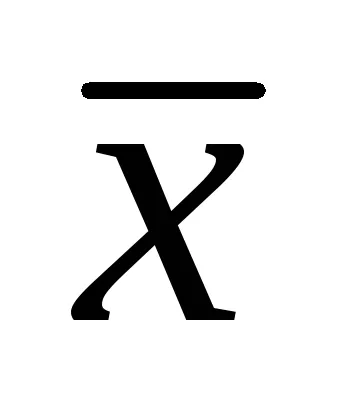




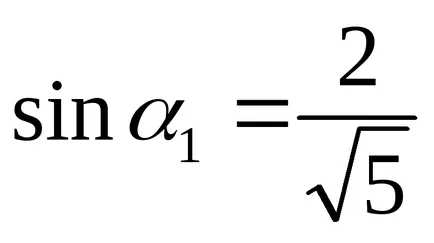

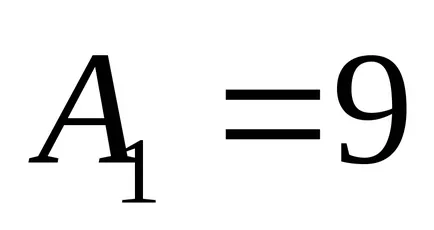
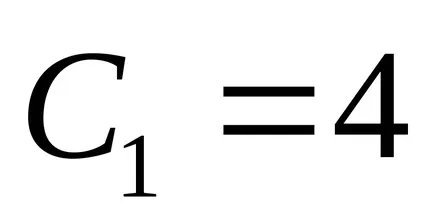
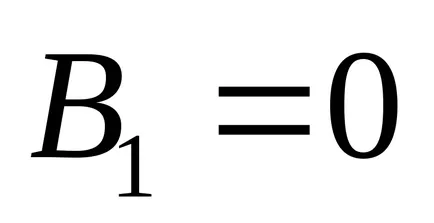
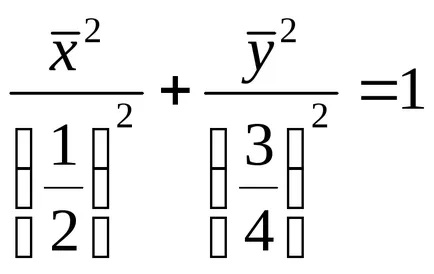
Megvan a kanonikus egyenlete ellipszis, félig tengelyek