2 mozgás kerületileg
Laboratóriumi munka № 2
Téma: „A tanulmány a testmozgás egy kört”
Célkitűzés: Annak vizsgálata, a feltételek egy egységes test körkörös mozdulatokkal. Run test gyorsulás kiszámítása felfüggesztve egy szál annak egyenletes mozgását kerületileg hatása alatt a gravitáció és a rugalmas erő. Ellenőrizze az eredményeket a számítási kísérletileg.
Felszerelés: menet egy labdát a lyukba, mérő vonalzó, papírlap, egy stopper.
Newton második törvénye teste mozog sebességgel υ egyenletesen egy r sugarú kör, ha a kapott minden erő a testre ható, merőleges a sebességvektor, és modulusa egyenlő: F = ma =
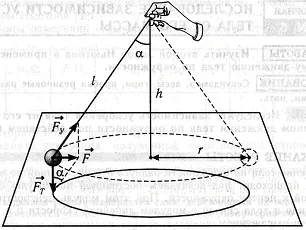
Amikor forgó test perifériás felfüggesztve szálak rajta vannak a nehézségi erő Fy FT és rugalmasságát.
Amint az ábrából látható, az eredő erő: F = Fm tg = mgtg.
Ezért, a centripetális gyorsulás, amikor a test mozog egy r sugarú kör alapján lehet kiszámítani, hogy a képlet a = tg.
Az, hogy a teljesítmény
1. Számítsuk ki a centripetális gyorsulása a labda lógott a szál hossza 30 cm, egyenletes mozgás sugarú kör 15 cm-re a általános képletű (1).
2. Határozza meg a centripetális gyorsulás a labdát kísérletileg. Erre a célra, egy papírlap, kör megrajzolásához r = 15 cm. Fektesse a lap az asztalon. Keresztül a menet léggömb, és a jelet a menet hossza L = 30 cm, számítva a központtól a labdát.
Vegyük a szál helyett a jelet, helyezze a labdát a közepén a kör által rajzolt. Fokozatosan letekercselés ballon, elérése annak egységes forgását a kerülete egy sugara 15 cm (lásd. Ábra.). Mérjük meg a t időt, amely alatt a labda teszi n = 20 fordulat.
Számítsuk ki a centripetális gyorsulás, ahol a képletben.
3. Hasonlítsa össze a számított és kísérleti ap ae értékeit centripetális gyorsulás. Megegyeznek? Hogy a következtetést.