4. fejezet A második és harmadik főtétele

Az entrópia (az grech.entropia- fordulat, átalakítás) - a koncepció volt először vtermodinamike hogy meghatározza az intézkedés visszafordíthatatlan energiaelnyelő. Az entrópia vstatisticheskoy fizika - az intézkedés a valószínűsége megvalósítása makroszkopikus állapot, vteorii információk - intézkedés a bizonytalanság kísérlet (teszt), esetleg eltérő eredményeket. Ezek az értelmezések az entrópia egy mély belső kapcsolatot.

1 entrópia. Termodinamikai entrópia értelemben

Lényegében az összes folyamatok nagyrendszerek visszafordíthatatlan.

Felmerül a kérdés: mi az oka lehet visszafordulni? Ez különösen furcsa, ha figyelembe vesszük, hogy minden a mechanika törvényei visszafordítható az időben. És mégis, senki sem látta, például törni egy váza spontán felépült a törmeléket.

A megoldás erre a problémára komplex jött a megnyitása új termodinamikai mennyiség - entrópia - és a nyilvánosságra hozatala csak fizikai értelemben.

A koncepció az entrópia volt először R. Clausius 1862-ben az egyik legcsodálatosabb felfedezések „az a toll hegyét”, azaz elméletileg.

Ennek ellenére és a hiányzó eszközöket, amelyek mérik az entrópia az anyag, ez a koncepció bizonyult rendkívül eredményes.

entrópia

bevezetni annak elemi növekmény mindkét

Meg kell figyelni, hogy a jellemzője ennek a képlet. Mint tudjuk,

nem a növekmény egy függvény, de miután a szétválás a hőmérséklet, Kiderült, kiderül a növekmény egy függvény (entrópia). ellentétben a hő, entrópiaugyanaz a funkciója, mint a hőmérséklet állapotban, belső energiavagy nyomás. A hő-rendszerEz attól függ, az átmenetet a kezdeti, hogy a végső állapot, a növekmény az entrópiateljesen független a folyamat, de csak a kezdeti és a végső állapot.

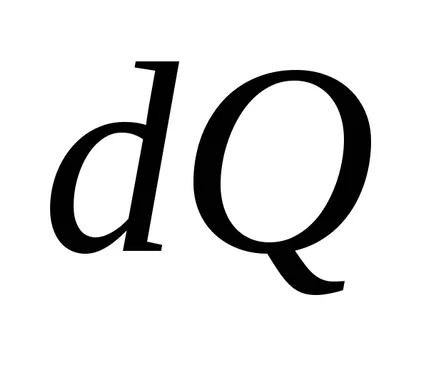
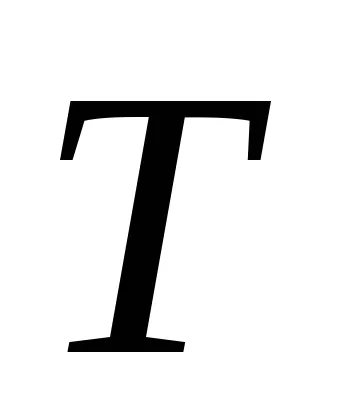
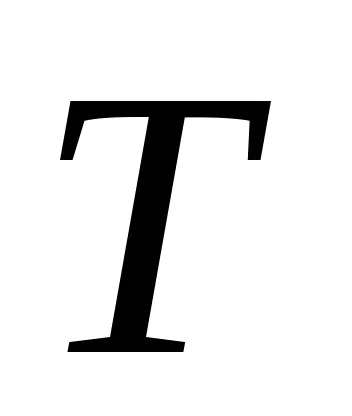
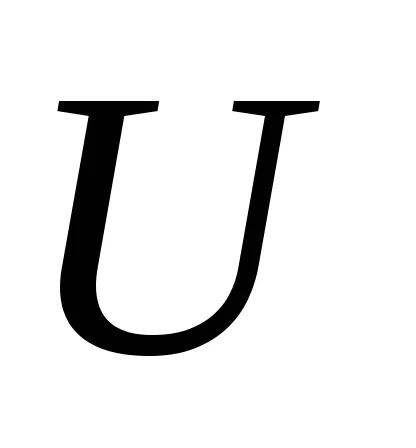
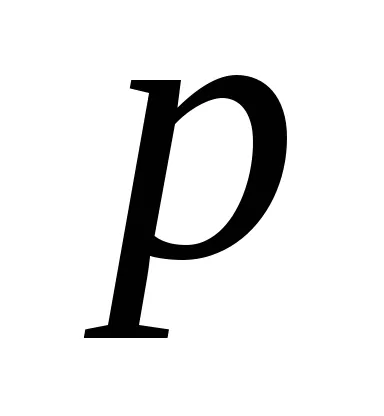
Így, egyensúlyi hőmérsékleten a hőátadó

elemi hőmennyiség egyenlő

.

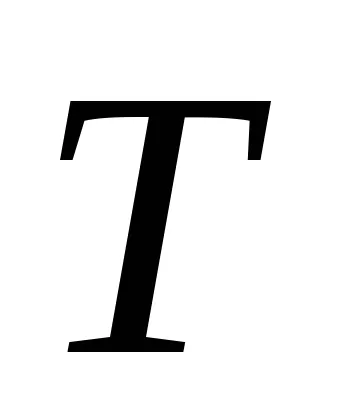
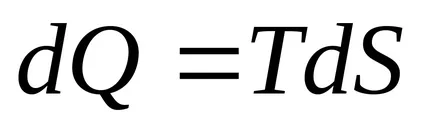
Az első főtétel felírható:

Hagyja, hogy a kezdeti állapotban a test hőmérsékletét

és a nyomásentrópiája, akkor szerint a (4.1) meghatározására az entrópiabármely más állapotban a hőmérséklet-és a nyomásMeg kell menni ebbe az állapotba kiindulva bármely egyensúlyi folyamat, folyamatosan halad egy kis test hőtmegfelelő hőmérsékleten.

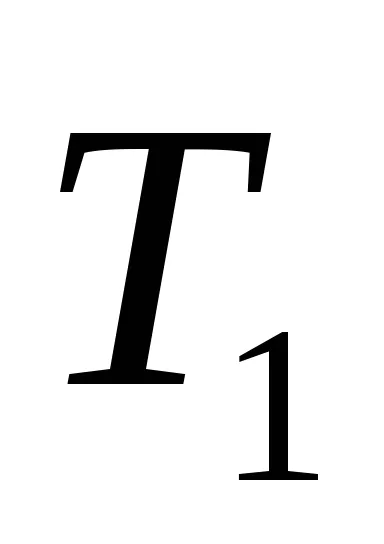
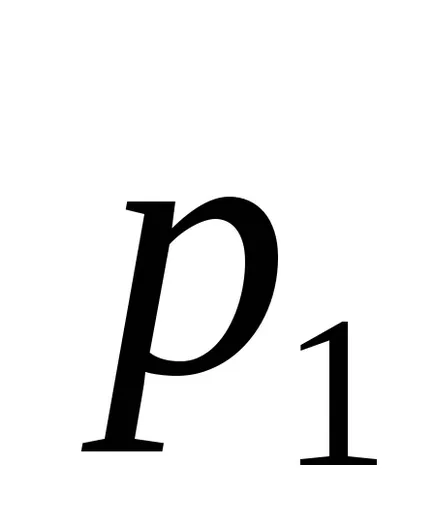
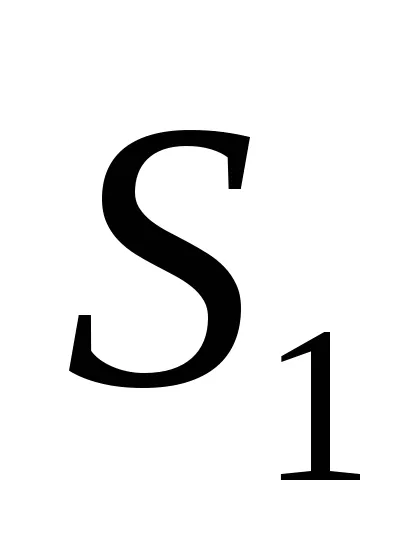
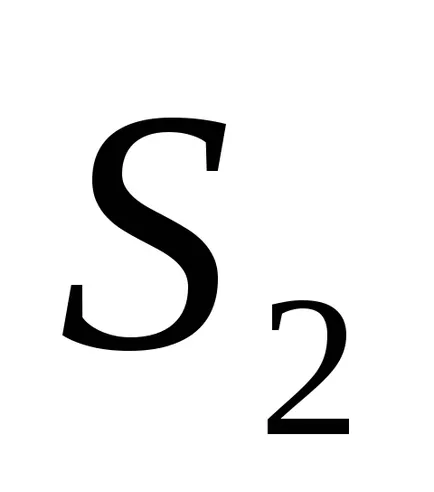
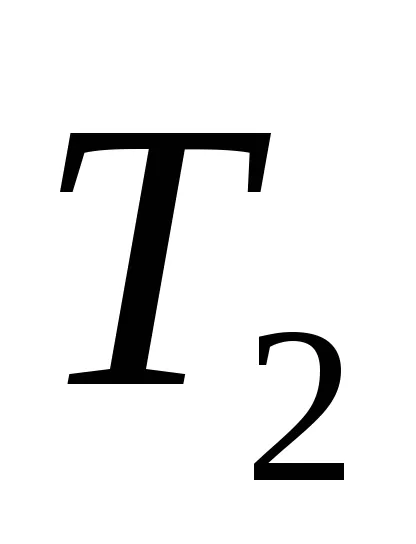
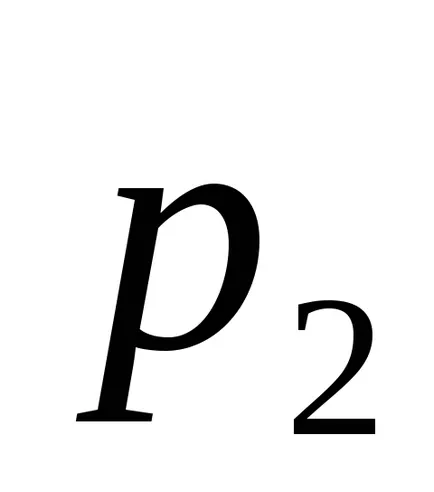
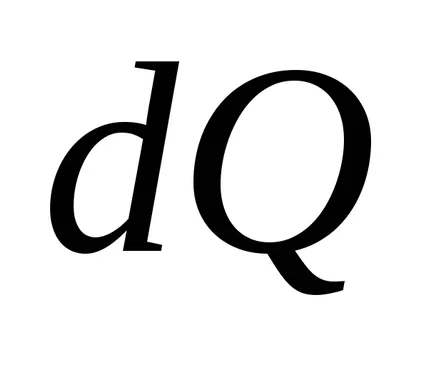
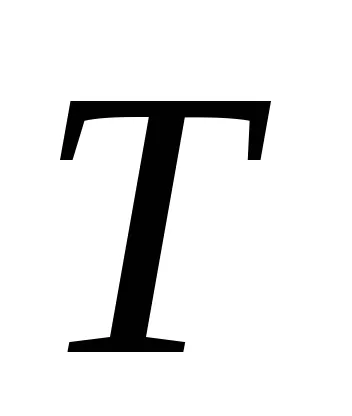
Ekkor az entrópia

Úgy kell kiszámítani, az általános képletű

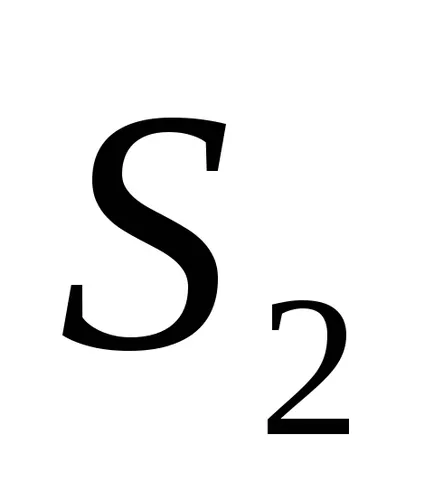
Közelebbről, az izotermikus folyamat (

)

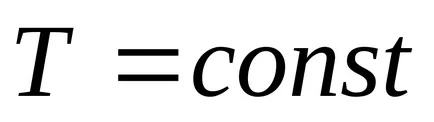
Mivel entrópia egy az állam, az integrál (4.3) nem függ az alakja a görbét, amely a folyamat, de csak az határozza meg a kezdeti és a végső állapot, azaz a határait integráció.

1) Az entrópia - értéke az adalékanyag: az entrópia a rendszer több testület az összege az entrópia az egyes szervek

.

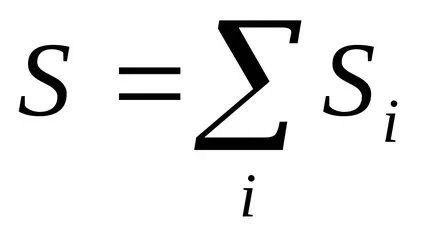
2) Az egyensúlyi folyamatok nélkül hőátadás entrópia nem változik.

Az adiabatikus folyamat

.

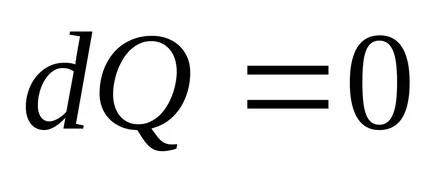
Ezért, az alábbi képlet szerint (4.1) egyensúlyi adiabatikus folyamat

és így. Ebben az összefüggésben az egyensúlyi adiabatikus izentropikus folyamat is nevezik.

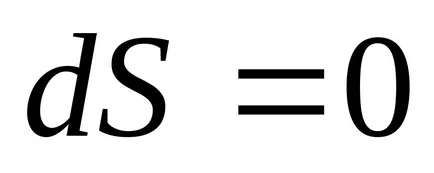
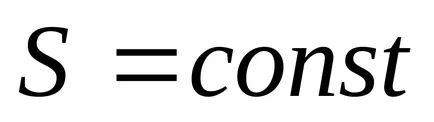
3) állandó térfogaton, az entrópia egy monoton növekvő függvénye a belső energia a test.

Sőt, amikor

van:, azért, hogy. de a hőmérsékletmindig pozitív. Ezért, ha, majd.

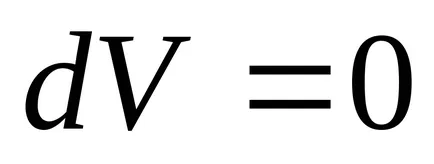
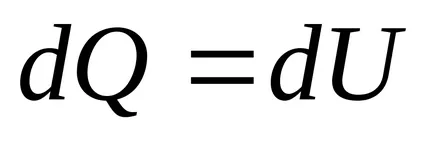
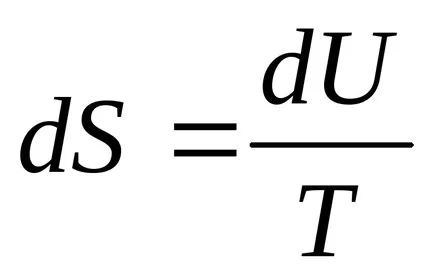
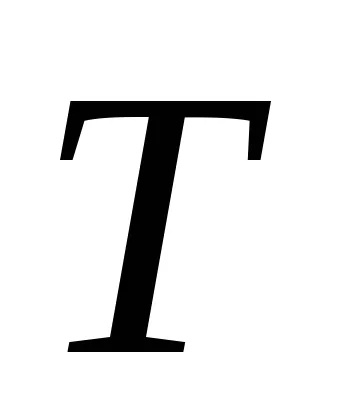
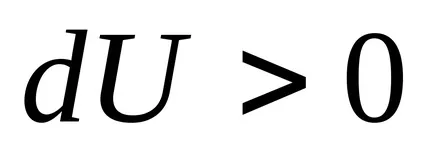
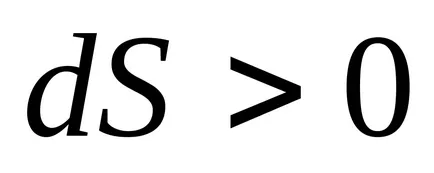
4) Az entrópia meghatározott csak akár egy tetszőleges konstans.

Szerint ugyanis (4.3) ki tudjuk számítani csak a különbség az entrópia

. Ez a különbség nem változott hozzáadásával entrópia tetszőleges konstans.

5) belső cél energia, mint a térfogat és entrópia függvényében

teljesen határozza meg a termodinamikai tulajdonságai homogén test.

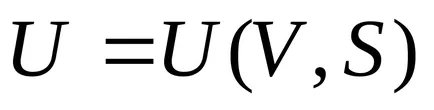
Valóban, a szabály alapján kell különbséget függvényében két változó

.

Figyelembe véve (4.2), amely

,

Ezek az egyenletek határozzák meg a hőmérséklet és a nyomás a belső energia

, hadefiniált függvényében térfogat és entrópia.

Figyeljük meg, hogy az egyenlő

Ez a legáltalánosabb hőmérséklet definíciója, tisztességes mind a klasszikus és kvantum rendszerek.

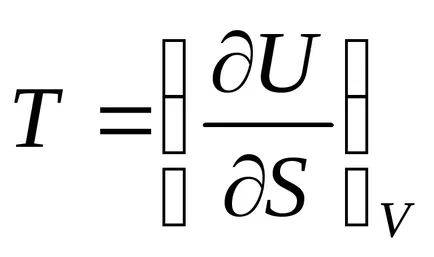
abszolút hőmérséklet

- Energia intézkedés a véletlen mozgását részecskéket.