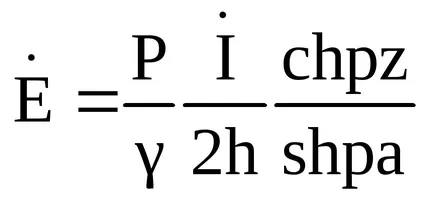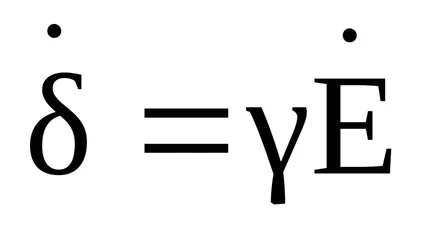5 váltakozó elektromágneses mező
5.1 munkaprogramja
Meghatározása egy változó elektromágneses mező. Basic egyenletek (Maxwell egyenletek) váltakozó elektromágneses mezőt. A kontinuitási egyenlet. Maxwell-egyenletek egy komplex számmal. Poynting tétel a pillanatnyi értékek, valamint egy komplex számmal. Váltakozó elektromágneses mezőt egy homogén, izotróp vezető közeg. Maxwell-egyenletek egy vezető közeget. Mágneses hatás kiváltására. Elektromos felületi hatást.
Alapok és 5,2 arány
1. A váltakozó elektromágneses mező (PEMP) - egy sor időben változó és összekapcsolt egymáshoz és így a villamos és mágneses mezők. Ez határozza meg a két vektor mennyiség - az elektromos térerősség

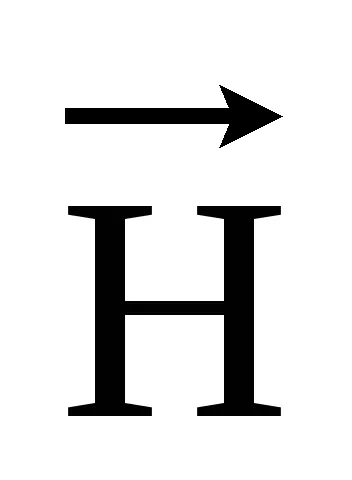
2. Maxwell-egyenletek. Process PEMP vizsgálatot végeztünk a Maxwell-egyenlet. Maxwell-egyenletek olyan rendszert alkot, négy egyenlet:
Először Maxwell egyenlet közötti kapcsolatot fejezi ki a forgórész mágneses mező és az áramsűrűség ugyanazon a ponton a pályán. A pillanatnyi értéke az első Maxwell egyenlet van írva a következő:

Két áramsűrűség az első része az egyenletnek: a vezetési áramsűrűség

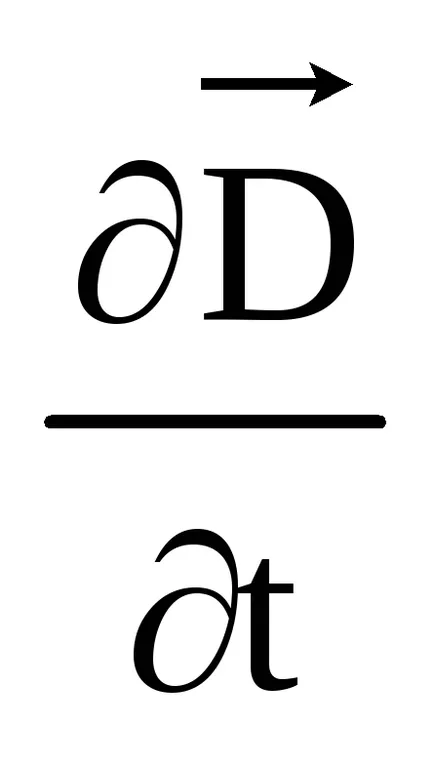
Ha megváltoztatja az E és H a szinuszosan időben használhatja a szimbolikus módszerrel rögzíteni, és az első Maxwell-egyenlet komplex függvénnyel
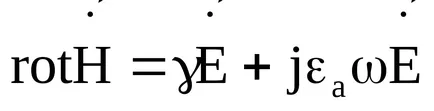
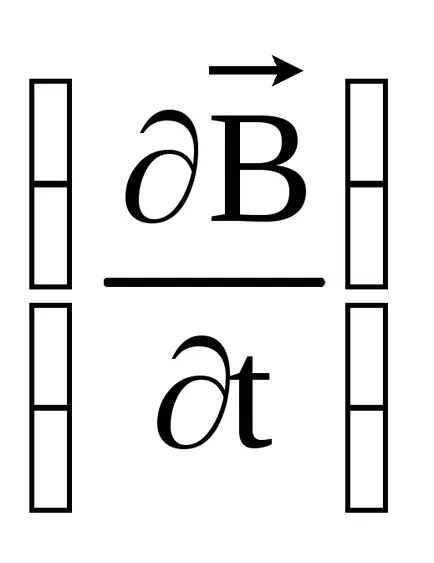
A második Maxwell egyenlet határozza meg a kapcsolat a forgórész a villamos térerősség, és változási sebessége a mágneses mező ugyanazon a ponton a pályán. Az azonnali értékek meg van írva a következő:

azaz bármilyen változás a mágneses térben, időben
Egy komplex számmal második Maxwell egyenlet

egyenlet
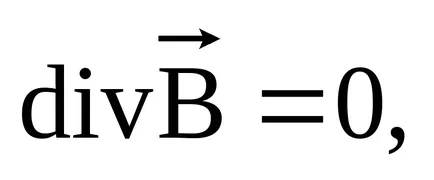
egyenlet

3.Uravnenie folytonosságot. teljes aktuális sort
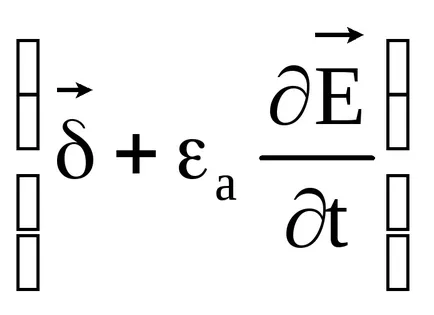
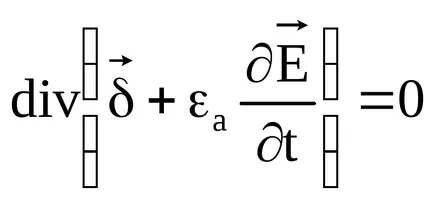
Ez az egyenlet felírható másképp
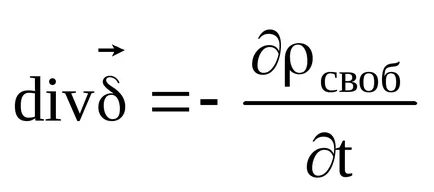
Ez az egyenlet is nevezik megmaradási törvénye igénybe. Ez a törvény azt jelenti, hogy az elektromos töltés elpusztíthatatlan, csak egyik helyről a másikra.
4. tétel Poynting.
Tétel Poynting ismerteti energia arány terén. Két nevezés: az első - pillanatnyi értékek, a második - egy komplex hátrány - a szinuszosan változó mennyiségben.
Poynting tétel a pillanatnyi értékek írt az alábbiak szerint:
.
A bal oldalon az egyenlet van egy áramlás a Poynting vektor

.
A jobb oldalon az egyenlet az energia

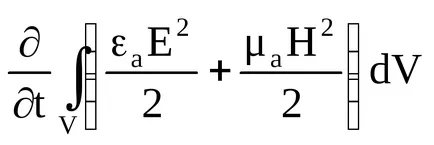
Poynting Tétel egy komplex számmal van:
.
Az első kifejezés a jobb - a hatásos teljesítmény, a második - reaktív. Következésképpen a Poynting tétel felírható a következőképpen:
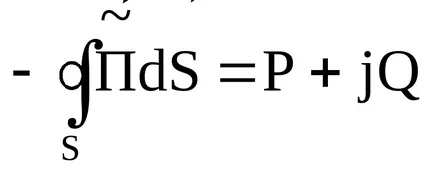
Az utolsó kifejezés
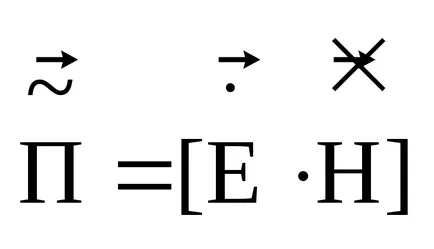
5. Maxwell-egyenletek egy vezető közeget.
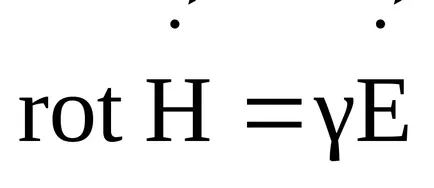
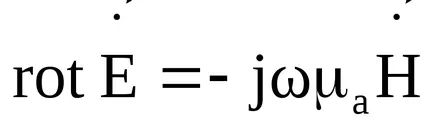
6. Egy sík elektromágneses hullám.
Repülővel elektromágneses hullám érti a hullám vektorok
A mágneses térerősség határozzuk meg:
,
ahol
Az elektromos térerősség:
,
ahol
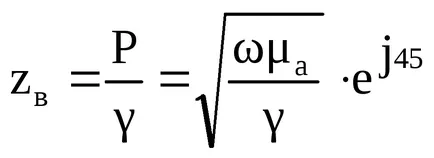
7. A behatolási mélység, és a hullámhossz.
A behatolás mélysége Δ észre a távolságot iránya mentén hullámterjedési (mentén a z-tengely irányában), amelyben az amplitúdó a beeső hullám E (vagy H) van faktorral csökken e = 2,71-szor. Tekintettel arra, hogy e = e -1 -KΔ. megkapjuk
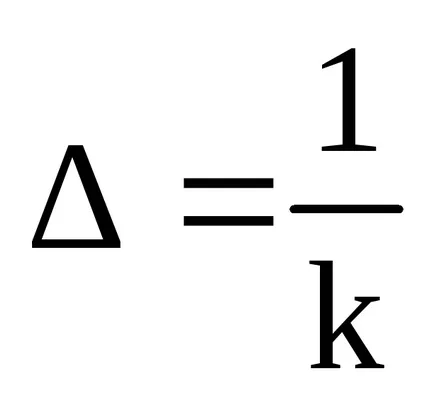
Under hullámhossz λ egy vezető közeget észre a távolságot iránya mentén hullámterjedési (mentén a z-tengely irányában), amelyben a fázis a oszcilláció változik 2π. Tekintettel arra, hogy: X- · κ = 2π, megkapjuk
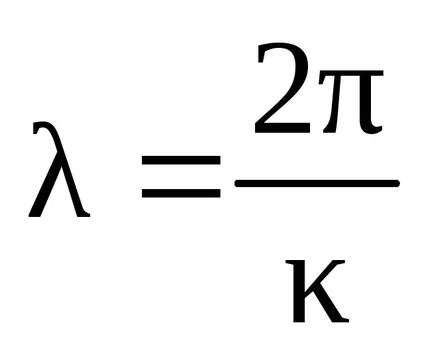
Under fázissebesség megérteni a sebességet, amellyel lenne szükség, hogy mozognak a Z tengely a vobbulációs ugyanaz volt a fázisban;

8. A mágneses felületi hatást.
Az a jelenség, egyenetlen mező eloszlását keresztmetszetében a hővezető által okozott csillapítás az elektromágneses hullám, mert terjed egy vezető közeget, azzal a megkötéssel, hogy a lap mentén irányul mágneses áramlás, az úgynevezett felszíni mágneses hatás. Ebben az esetben:

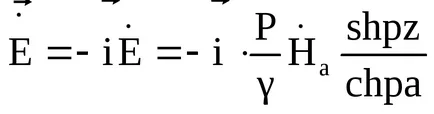
Ha azt feltételezzük,
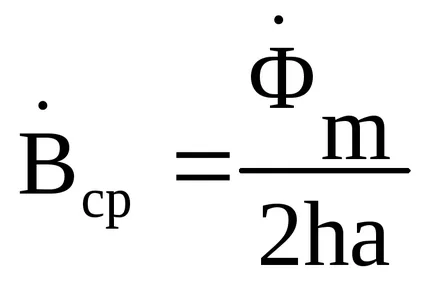
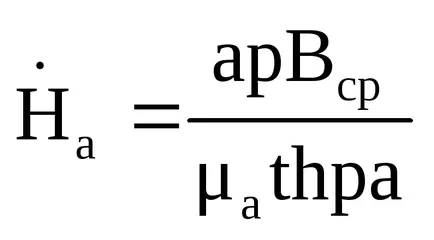
9. Amikor az elektromos hatás mentén a lemez felületén (a gumiabroncs) irányul szinuszos aktuális frekvencia ω. Ebben az esetben, a mező belsejében a lemez határozza meg a képletek: