A fázis az oszcilláció
Bemutatjuk a másik mennyiség jellemző harmonikus rezgések - fázisú hullámok.
Egy adott rezgések amplitúdójának a oszcilláló test koordináták bármely időpontban egyértelműen meghatározzák a koszinusz vagy szinusz érv: φ = ω0 t.
A mennyiség φ, álló jel alatt a koszinusz vagy szinusz függvény, az úgynevezett rezgési fázisban. által leírt ezt a funkciót. Fázis kifejezve szögmértékegységben - radián.
Phase függ nemcsak a koordináta értékét, de az értéke más fizikai mennyiségek, mint a sebesség és a gyorsulás, a változó és harmonikusan. Ezért azt mondhatjuk, hogy a fázis határozza meg egy adott amplitúdójú rezgési állapotát a rendszer bármikor. Ez az értelme a koncepció fázisban.
Rezgések amplitúdója azonos, és frekvenciák változhat fázisok.
Az arány azt jelzi, hogy hány időszakok telt kezdetétől oszcilláció. Bármilyen értéke az idő t, kifejezett időszakok száma T megfelel a fázis értéket φ, radiánban. Így, miután az idő múlásával (egy negyed periódus) után egy fél időszak φ = π, miután az egész időszakban, és φ = 2π t. D.
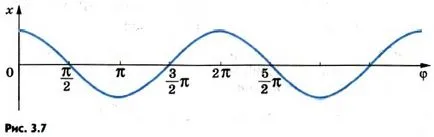
Leírható a diagramon koordináta függvényében az oszcilláló pont nem az idő, és a fázis. Ábra 3.7 ábrán ugyanaz a cosinus hullám, ahogyan 3.6 ábra, de ahelyett, hogy a vízszintes tengely az időt jelöli, különböző értékeket fázis φ.
Bemutatjuk harmonikus rezgések segítségével szinusz és koszinusz. Azt már tudjuk, hogy a harmonikus rezgéseket a test koordináta idővel változik a törvény szerint a koszinusz vagy szinusz. Miután a koncepció bemutatása fázis megvitatni ezt részletesebben.
Sine koszinusz érv eltér műszakban, amely megfelel, amint látható egyenletből (3,21), egy időintervallumot egyenlő egy negyed időszak:
Ezért ahelyett, hogy a X képletű = Xm cos ω0 t képlet használható, hogy leírja a harmonikus rezgéseket
De ez a kezdeti fázisban van. t. e. fázis értéket t = 0 nem egyenlő nulla is.
Normálisan a szervezet rezgések csatolt egy rugó vagy inga mi gerjeszti, így az inga test egyensúlyi helyzetbe, majd elengedve. Az elmozdulás az egyensúlyi helyzetből a lehető a kezdeti pillanatban. Ezért, hogy leírja oszcilláció sokkal kényelmesebb használni a képlet (3,14) használata révén koszinusz mint képletű (3,23) használatával sinus.
De ha gerjeszti oszcilláció test nyugalomban rövid távú ösztönzést, a test koordinátáit a kezdeti pillanatban nulla lenne, és koordinálja időbeli változása, hogy könnyebb lenne leírni útján sine t. E. Formula
mivel ebben az esetben a kezdeti fázis nulla.
Ha a kezdeti időt (t - 0), a fázis oszcilláció φ, akkor a rezgés az egyenlet felírható a
fáziseltolódás. Oszcillációkat által leírt (3,23) és a (3.24) különböznek egymástól csak a fázisban. A fáziskülönbség, vagy, ahogy gyakran mondják, a fáziseltolódás a rezgések. 3.8 ábra mutatja a grafikonok a koordináta az idő két harmonikus rezgések eltolt fázisban. 1. ábra megfelel a rezgések követ szinuszosan: Xm = x sin ω0 t, és a 2. ábra - oszcillációk által végrehajtott koszinusz törvény:
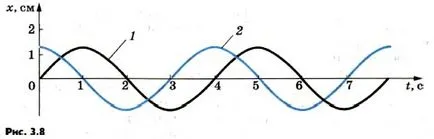
Ahhoz, hogy meghatározzuk a fáziskülönbség a két rezgés kell oszcilláló nagysága mindkét esetben kifejezve azonos trigonometrikus funkció - a szinusz vagy koszinusz.
Kérdések bekezdés
1. Mi az úgynevezett harmonikus rezgéseket?
2. Hogy a gyorsulás és koordinálja a harmonikus rezgéseket?
3. Hogyan ciklikus rezgési frekvenciája és időtartama rezgések?
4. Miért gyakorisága rezgések a szervezet, amelyhez olyan rugó függ a tömeg, és a frekvencia oszcilláció egy egyszerű inga független a tömeg?
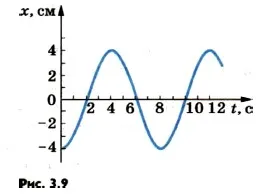
5. Mik az amplitúdók és időszakok három különböző harmonikus oszcilláció, melynek grafikonok ábrákon mutatjuk be 3,8 és 3,9?