A fő feladatok a 2. félév

Egyenlet (4.7) lehet tekinteni, mint egy közvetlen egyenlet, amelyben a koordináták már polárkoordináták x 0 a 0 Következésképpen, forgása során a nulla vonal az M pont mozog a pole K-l sejtvonal. egyenlettel meghatározott (4,7). Mivel a jelenlegi

Az X koordináta. és polárkoordinátákban x 0 y 0 tartalmazza egyenlet (4.4) teljesen egyformán, akkor a fordítottja helyzetet, azaz ha mozog egy egyenes rúd nulla vonal körül forog egy bizonyos ponton rajta.

Abban a helyzetben a pólus pontokon M 1 és M 2 K-l sejtvonal (Fig.4.4), azaz a x és y tengelyek, illetve veszi nulla vonal helyzetét n 1 -n 1 és n 2 -n 2. metszéspontja, amely meghatározza a forgási középpont C. Tény, hogy a helyét a pólusok az egyik tengely metszéspontja a nulla vonal a másik tengely, szerint a kifejezést (4.5) tart végtelenbe, azaz null vonal párhuzamos a másik tengely.

4.2. részben a kernel.

Amikor excentrikus kompressziós rudak, ahol az anyag gyengén védőréteg nyújtás, hogy szükséges annak biztosítása, hogy nem voltak keresztmetszeti húzófeszültséget. Ebből a célból, a nulla vonalat kell állapítani kívül részben, vagy extrém esetben vonatkozik részén keresztezése nélkül meg (4.3 ábra).

Kiderült, hogy az egyes keresztmetszet lehet kialakítani annak síkjában zárt hurok, amely a tulajdonság, hogy amikor a hosszirányú erőhatás pontot belsejében vagy határán a kontúr keresztmetszetben, amelynek feszültsége azonos előjelű. Része a vágási sík által határolt ez kontúr, az úgynevezett mag a szakasz. Ha a kimenet a nyomóerő a mag, a keresztmetszet a húzófeszültség.

Ahhoz, hogy a mag előállítására a szakasz a következőképpen kell eljárni. Mi határozza meg a helyzetét a nulla vonalat úgy, hogy megérinti a rész, soha átkelés is, és megtalálni a megfelelő pólus vagy pont az erő alkalmazását. Amikor ez a feszültség szakasz lesz a ugyanaz a jel (4.3 ábra). Fürdőzés után egy család érintő a keresztmetszet, kapunk egy sor megfelelő oszlopok nekik pályája amely a körvonal (kontúr) részben a kernel.

Ha a szakasz sokszög alakja van, a keresztmetszet a mag is egy sokszög. Tegyük fel például, mivel a keresztmetszete ábrán látható. 4.5, a fő tengelye x. y.

Ahhoz, hogy a mag előállítására a szakasz tölteni öt érintői a kontúr a keresztmetszet is elegendő, négy, amelyek egybeesnek az AB oldalára, AF, EF, és az ED, és az ötödik összekötő pont B és D. A tangens egybeesik a BC és CD oldalán, akkor nem azért, mert Keresztfűrészek . Mért vagy számított lefoglaló az érintő 1-1, ..., 5-5 az x és y tengely. helyett a értékei szegmensek a képletben (4.6), definiáljuk a koordinátái x 0 y 0 öt pólusok 1, 2, ..., 5, megfelelő öt rendelkezések

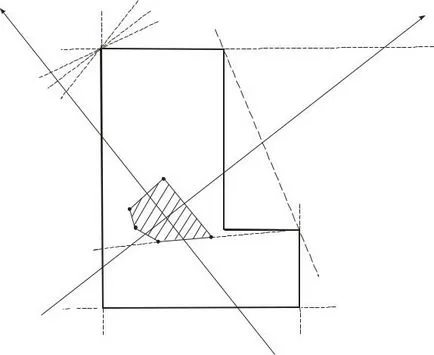
null sor, és a telek a pólusok a rajz. Tangens 1-1, ami megfelel a rúd 1 átalakítható 2-2 helyzetben, forgatva pont körül A. Ebben az esetben, a pole szerinti 1 a fenti bizonyult mozgatható szerint egy egyenes vonal, és ennek eredményeként a forgási érintőlegesek 2. pontban.

Ennélfogva, az összes pólus megfelelő közbenső pozíciók közötti érintő 1-1 és 2-2, lesz található a sorban 1-2. Hasonlóképpen, mozgó tangensét 2-2 3-3 helyzetbe forgatva az F. pontban így egy második oldalrésze 2-3 magok, és így tovább. Ez azt jelzi, hogy a mag keresztmetszete egy olyan sokszög, ami elég ahhoz, hogy létrejöjjön, hogy csatlakoztassa a pólusok 1,2, ..., 5 egyenes.

Kanyarodáskor a nulla vonal pozícióban VA AF pozíciójának megfelelő pólus útvonalú részéhez 1-2 egybeesik, természetesen, a fémcsövet a sejtmagban.

Okozása a vonal 1-2 rajz vonalszakaszokkal, hogy ismételjük meg a műveletet egymás az összes többi csúcsot részben. Ezután a beállított metsző egyenes 1-2, 2-3, 3-4, ... biztosítja a magrészben. A metszéspontjait ezeket a sorokat, vagyis A tetején a mag egyezik egyidejű a nulla vonal keresztmetszeti oldalán.

Nyilvánvaló, hogy a sokszög alakú keresztmetszete van a mag is egy sokszög, amelynek csúcsai pólusok megfelelő Nullvonalak egybeeső a sokszög oldalainak.

Ahhoz, hogy a mag előállítására a szakasz a sokszög, hogy:

1) található a fő központi tengelye a tehetetlenség és a megfelelő forgási sugarak;

2) minden egyes oldalán a szegmensek, hogy megtalálja a és b. levágja annak kiterjesztését az x és y tengely;

3) koordinátáinak kiszámításához a csúcsok magrész képletekkel (4,6) .:

4) csatlakoztassa a felső mag vonalak.

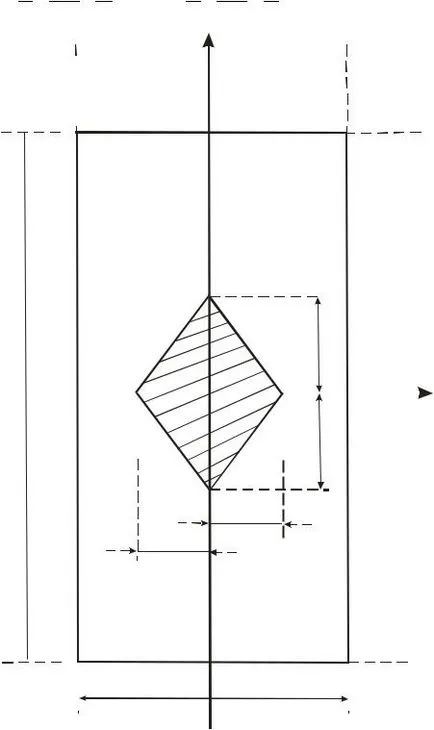
Különleges esetek. Példa 4.1. A négyszögletes keresztmetszetű (4.6 ábra.).

A téglalap kontúr tölteni négy érintők, amelyek párhuzamosak a fő tengelye a keresztmetszet, és így a megfelelő sávok lesz található a fő tengelyek.

Mi először meg az értékeket a négyzetek sugarak tehetetlenségi nyomatéka:

Ezért a sugara mag a szakasz 1 e i 2 R 2 R 2.

Ha a belső sugara a gyűrű növekszik, amivel együtt az értéket az r sugár R. E 1 magrészben hajlamosak az értéket R2.

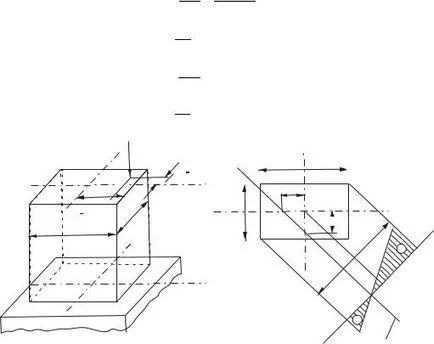
Példa 4.5. oszlopon négyszögletes keresztmetszetű (ábra. 4.8 a) van betöltve a kifejtett erő a P pontban A., amelynek koordinátái y 0 és 5 cm

0 x 12 cm-es. Megtalálják a helyzet a semleges tengely, és épít diagramok a normális

keletkező feszültségek a keresztmetszete az oszlop. Saját tömeg elhanyagolt oszlopban.

Határozat. Meghatározza a geometriai jellemzőinek szakasz:

F ab 30 20 600 cm 2;

Számított oszlop áramkör

Képletek (4.3) meghatározzák szegmensek B és A. semleges tengelye elfogja a tengelyek y és x:

b i x 2 / y 0 33,3 / 5 cm 6,66; A I y 2 / x 0 75/12 6,25 cm.

Határozza meg a feszültség 0 a tömegközéppontja a keresztmetszet (Y = 0):

0 P / F 150/600 0,25 kN / cm2.

Ábra. 4,8, b a kapott értékeket a és b megtalálják a helyzet a semleges tengely nn. .toy tengelyére merőleges egyenes vonal mm. Ezután, a súlypont a carry szakasz párhuzamos egyenes a semleges tengely a metszéspontja a vonal 7 mm. Ebből a szempontból elhalasztásának ordináta 7- 8 egyenlő a feszültség 0 (a kiválasztott skála). Ezután a pont 9

(Semleges tengelye keresztező egyenes mm) és a 8. tartsa egy egyenes vonal, amely a vonal végeit összekötő stressz diagram.

4.6 példa. Építsünk egy része a mag a keresztmetszet formájában márkák ábrán látható. 4.9.

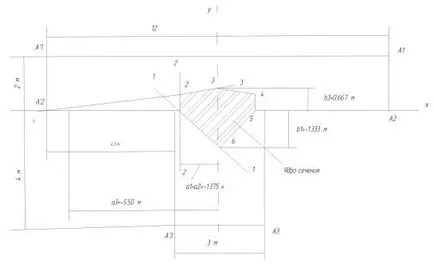
Kernel I-gerenda rész

A tömegközéppont a keresztmetszet található azon a ponton O. A geometriai jellemzői a szekció: F 36 m 2 J x 96 m 4. J y m 4.

Határozat. Amikor a pole 1 egy pont (koordináták Y A és 1 2 m 1 X A 6 m) elfogja a nulla vonal a koordinátatengelyeken egyenlő:

b 1 i x 2 / Y A 1 J x / FY A 1 96 / (36 2) 1,333 m;

egy 1, i y 2 / X A 1 J y / FX A 1 297 / (36 6) 1,375 m.

A értékek ezeket a szegmenseket ábra. 4.9. épült a nulla vonalat 1-1. a

A pólus 2. pontban (a koordinátákat Y A 0 és X A