A fordulatok száma egységnyi idő alatt a reciproka az időszak
Ez könnyű megszerezni a kapcsolat a Sarki és lineáris sebesség pont.
Amikor mozog körív tag kapcsolatos végtelenül forgási arány. Itt van.
Behelyezi (1), azt találjuk, hogy a lineáris sebessége a modul egyenlő
Általános képletű (4) kapcsolódik a nagysága a szögletes és lineáris sebesség.
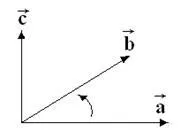
Egy általánosabb kapcsolatban kitűnik a rajz, ahol a lineáris sebesség vektor, a termék a szögsebesség -, és a sugár vektor pontok:
1. Egy vektor proizvedeniemvektorov nevezett vektor, amelynek nagysága megegyezik a terület a paralelogramma által alkotott vektorok faktor, és a sajátvektor és a forma egy jobbkezes vektorok.
Szöggyorsulással - az az idő, származéka szögsebesség (vagy második idő szerinti deriváltja a forgásszög)
3. Példák a számítás a kinematikus a jármű jellemzőit.
A verseny autó halad egyenes pályaszakasz, így annak gyorsulás lineárisan növekedett az első és a 10c eléri azt az értéket 5 m / s 2 elhanyagolása saját mérete és súlya határozza meg a végén a 10. másodpercben: 1) a jármű sebességét; 2) telt el az útjukat.
Gyorsulás lineárisan növekszik, és az ismeretlen tényező az arányosság - m / s.
By hipotézis mozgás - egyenes vonalú, így a sebesség -
A megtett távolság egyenes vonalú mozgás lesz egyenlő:
1) általános képletű (1) - m / s; 2) általános képletű (2) - m.
Pálya jármű modell kikötve forog frekvenciával Hz. Megszűnését követően rudak, modell, ami fordulat, megállt. Figyelmen kívül hagyva a saját méretét és súlyát az autó modell, meghatározza annak szöggyorsulással - ha feltételezzük, hogy a gátlás ravnozamedlennym.
Mivel gátlása ravnozamedlennym elfogadott, a forgásszög -
ahol a szögletes forgási frekvenciája, Hz (2).
A végső szög értéke - rad (3).
A végleges értéke körfrekvencia - így a kapcsolatban -, ahol a leállási időt, hogy (4).
Behelyettesítve (1) egyenlet kapcsán (2), (3), (4), azt találjuk, hogy rad / c.
Megjegyzés. Az oldatot állíthatjuk elő általános formában, feltételezve, hogy a meghatározott általános kifejezések - (2 ÷ 4). Ezután rad / c.