A geometriai jelentését határozott integrál - studopediya
Legyen egy - egy folytonos függvény az intervallumon. Ez a funkció nem negatív, azaz a.
Görbe vonalú trapéz - az
ábrára, amely alulról korlátos tengely. felső grafikon
funkciót. oldalán a függőleges vonalak. .
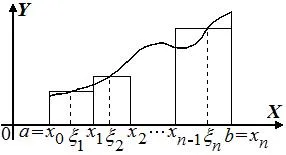
Tekintsünk egy tetszőleges partíció T
Válassza pontokon minden részleges intervallumban a partíciót. A kilépési munka értéke egy pontot a hossza a részleges szegmens téglalap terület geometriailag a bázissal hosszát és magasságát. Akkor az összeg a Riemann-integrál az a terület, lépésről-szerű alak alkotja ilyen téglalapok. Amikor köszörülés a partíció, hogy van, amikor. területe lépés-szerű alak hajlamos a területet a görbe vonalú trapéz:
A geometriai jelentése a határozott integrál.
A határozott integrál egy nem-negatív folytonos függvény
intervallumon megegyezik a terület a görbe trapéz alatt fekvő grafikonja ez a funkció.
Néha lehet számítani a határozott integrált csak geometriai jelentését.
Példa 1. Számítsuk ki az integrál.
Az integrandus folytonos és pozitív az intervallum
. Togdavelichina szerves szám alatti terület függvény grafikonját. Ez a szám a szokásos trapéz területe formula trapéz találni
Példa 2. Számítsuk ki integrál.
Integrandus folytonos és nemnegatív az intervallumon. Togdavelichina szerves szám alatti terület függvény grafikonját. Ez a szám egy negyed kör sugara.
Körrel terület formula, azt találjuk, hogy az érték az integrál