A henger alakú edényt folyadék szintje eléri a milyen magasságban marad szinten

A hengeres tartály, a folyadék szintje eléri a 16 cm-es. A milyen magasságban lesz a folyadék szintje, ha annak öntsük a második hengeres tartály, amelynek átmérője 2-szer nagyobb, mint az első átmérő? A válasz centiméterekben kifejezve.

Henger térfogata V = πR 2 órán át.

Az első esetben, folyadék térfogata egyenlő V = 16πR 2.

Ha az átmérője a második edény 2-szer nagyobb, mint az átmérője az első edény, és a sugara a második tartály 2-szer nagyobb, mint a sugara az első hajó. Ezért, miután a Transfusion folyadékot a második edénybe, annak térfogata lehet képlettel számítottuk ki:

V = π (2R) 2 h = 4πR 2 H, ahol h - magasság kívánt.

Mivel a folyadék térfogata állandó marad transzfúzió, ezek a mennyiségek a következők:

16πR 2 = 4πR 2 H,

Hengerek és kúpok közös alap, a teljes magassága. Számítsuk ki a térfogatát, a dugattyú, amikor a térfogata a kúp egyenlő 20.

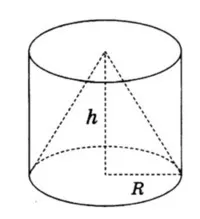
Cone magassága egyenlő a magassága a henger és kúp sugara megegyezik a sugara a henger (lásd. Ábra.).

A kötet a kúp egyenlő vk = (1/3) πR 2 h = 20.

A kötet a henger Vts = πR 2 3Vk = h = 3 * 20 = 60.

Ennélfogva, a térfogata a henger 3-szor nagyobb, mint a térfogata a kúp és egyenlő 60.

Hengerek és kúpok közös alap, a teljes magassága. Számítsuk ki a térfogatát, a dugattyú, amikor a térfogata a kúp egyenlő 19.

Cone magassága egyenlő a magassága a henger és kúp sugara megegyezik a sugara a henger (lásd. Ábra.).

A kötet a kúp egyenlő vk = (1/3) πR 2 h = 19.

A kötet a henger Vts = πR 2 3Vk = h = 3 * 19 = 57.

Ennélfogva, a térfogata a henger 3-szor nagyobb, mint a térfogata a kúp és egyenlő 57.

A rendszeres négyszögletes piramis magassága megegyezik a 2. oldalsó széle 4. Keresse a hangerőt.

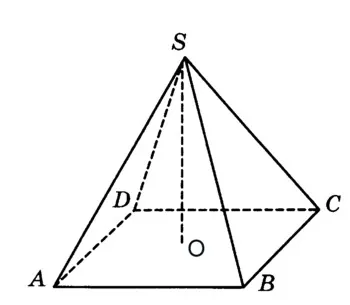
A kötet a piramis egyenlő V = (1/3) H. Sosn

H = SO = 2 állapot, SC = 4.

Az alap szabályos négyszögletes piramis egy négyzet. Mi megtalálja az utat, azaz találni AB.

SOC derékszögű háromszög a Pitagorasz-tétel, van:

SC 2 = SO 2 + OC 2

OC 2 = SC 2 - SO 2,

OC 2 2 = 4-2 = 2 12,

OC = √ (12) = 2√3,

AC = 4√3, AC 2 = 48.

A ABC derékszögű háromszög (tekintettel arra, hogy az AB = BC) a Pitagorasz-tétel, van:

2 AC = AB + BC 2 2 = 2AB 2

48 = 2AB 2. AB 2 = 24.

V = (1/3) * 24 * 2 = 16.

Hengerek és kúpok közös alap, a teljes magassága. Számítsuk ki a térfogatát, a dugattyú, amikor a térfogata a kúp egyenlő 12.

Cone magassága egyenlő a magassága a henger és kúp sugara megegyezik a sugara a henger (lásd. Ábra.).

A kötet a kúp egyenlő vk = (1/3) πR 2 h = 12.

A kötet a henger Vts = πR 2 3Vk = h = 3 * 12 = 36.

Ennélfogva, a térfogata a henger 3-szor nagyobb, mint a térfogata a kúp, és egyenlő a 36.