A koncepció a három vektor
17) A vegyes termék vektorok. Tulajdonságok és geometriai jelentése. Egy síkban vannak vektorok.
Vektor nazyvayutsyakomplanarnymi. vagy ha hazudnak ugyanabban a síkban vagy párhuzamos síkokban.
Tulajdonságok A kevert termék.
1) kevert termék [AB] c egyenlő térfogatának a paralelepipedon alakult egy közös felső megadott vektorokba a, b, c, ha alkotnak egy jobbkezes vagy szám, szemben ez a mennyiség, amikor abc - bal tripla. Ha a, b és c egy síkban vannak, majd a [AB] C = 0.
a) Ha a, b és c egy síkban vannak, akkor a vektor [AB] merőleges síkot a és b vektorok, és ezért, [ab] c. Ezért, [ab] c = 0.
c) Ha a, b, c nem egy síkban, [ab] c = | [AB] || C | = S # 903; | c | COS # 966;, ahol # 966; - közötti szög az a és [ab]. Ekkor | c | cos # 966; - magassága megfontolás alatt a doboz. Így, [ab] c = V, ahol a választás a jel függ közötti szög az a és [ab]. Az az állítás bizonyított.
Sőt, mindkét fél a kötet az azonos perellelepipeda. Ezért, a helyzet vektor zárójelben a kevert termék nem fontos, és annak kijelölése zárójelben nem. abc.
Bizonyítás. A koordináta-megadás skalár és vektor termék, tudjuk írni:
[Ab] c = (Ya Zb - Yb Za) Xc + (Xb Za - Xa Zb) Yc + (Xa Yb - Xb Ya) Zc =
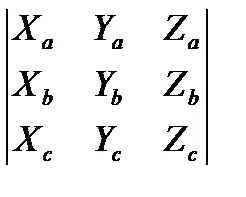
1. példa találunk a skalár hármas terméket vektorok a = b =, c =. Ahhoz, hogy ezt elérjük, kiszámítja a meghatározója a koodinat:
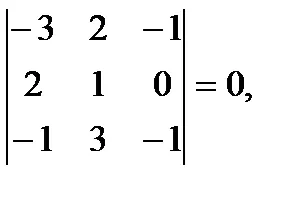
Polár koordinátarendszerben