A megoldás (konverzió) a szimplex tábla Online (általában egy téglalap) (döntés a legfelsőbb feladatok

Úgy véljük, részletesen, hogyan újraszámolt simplex táblázatokat (például egy ismétlés). Legyen egy szimplex táblázat látható az 1. ábrán. Mi oldja meg a problémát, hogy maximalizálják a célfüggvényt. Lehetővé teszi az oszlop megfelel a változó x2. és megoldása stringváltozó x3 (piros számok) a metszésvonaluknál megengedő cella (szürke háttérrel). Az első dolog, amit tennie kell -, hogy cserélje ki az alapvető változót. Felbontás vonal mutatja, amelyben a változó, hogy származhat alapján (ebben az esetben, x3), és lehetővé teszi az oszlop mutatja, hogy melyik változó lép alapján (ebben az esetben, x2). 2. ábra tény cserélni az alap variábilis szakították a kék vonalon.

Most újratervezi az elemek sorban állás felbontásban. Egyszerűen ossza mindegyikük egy engedélyezze elem (4 példánkban). És az összes elemet, amely lehetővé teszi az oszlop nulla, kivéve tagja sorban állás felbontásban. (Lásd: 2. ábra)

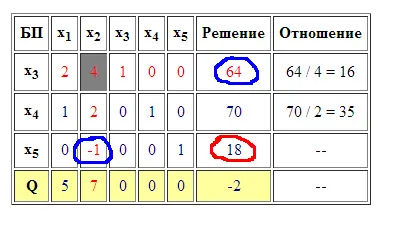
A visszamaradó sejteket az asztal (kivéve az oszlop „arány”) vannak átszámítva az úgynevezett szabály a téglalap. értelmében, amely a legjobban érthető példa. Tegyük fel, hogy újraszámolja a tétel bekarikázott piros vonallal az 1. ábrán. Értelmi tartjuk vele a függőleges és vízszintes, hogy a kereszteződés, a felbontás felhatalmazza a sort és az oszlopot. Elements állt a kereszteződésekben a kék bekarikázott áramkörök (lásd az 1. ábrát). Az új érték a „vörös” cella egyenlő lesz az aktuális érték az elem mínusz a termék a „kék” osztva az engedélyezését ( „szürke”) elem (lásd 1. ábra). Ie. 18 - (64 * -1) / 4 = 34. Itt a jel "*" egy szorzás művelet.
Írunk az új értéket a helyére (lásd 2. ábra piros keret).

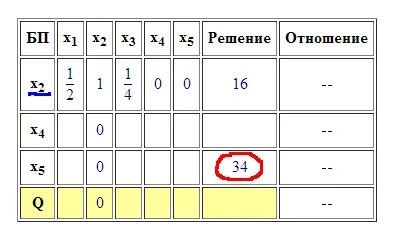
Ezzel a szabály, akkor töltse ki az üres táblázat elemei (oszlop kivételével „ratio”), lásd 3. ábra. Aztán meg egy új oszlopot lehetővé teszi. Ehhez vizsgálni a string „Q”, és mivel a mi feladatunk, hogy a maximális, ott találjuk a legnagyobb pozitív elem. ő határozza lehetővé oszlopon. A mi esetünkben ez 3/2. Minden bemutatott elemek rezolváló oszlopon pirossal jelöltük (lásd a 3. ábra). Ha ezek után a következő iteráció a string „Q” nem lesz pozitív elemeket - ami azt jelenti, hogy az optimális megoldás születik, az iterációs megszűnik. Ha az volt a célunk, hogy legalább lehetővé teszi az oszlop fogja meghatározni a minimális negatív elemek és ha miután a következő iteráció a string „Q” nem jelenik meg a negatív elemeket, akkor az optimális megoldás születik.

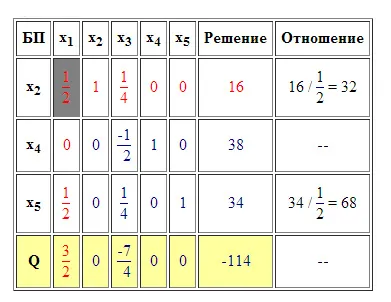
Most töltse ki az oszlop „Attitude”. Ehhez, a megfelelő (állva az ugyanabban a sorban) oszlopon elem „oldat” megosztani a megfelelő elemet, amely lehetővé teszi az oszlop (lásd 3. ábra). Megjegyzés. hogy a műveletet csak a pozitív elemeket, amely lehetővé teszi az oszlop és a vonal „Q” nem vesz részt ebben a műveletben. Ha ezek után néhány iteráció a kiadás oszlop nem lesz pozitív elemeket, ez egy lehetetlen feladat, figyelembe véve az objektív függvény korlátos, iteráció megáll.

A feltöltés után az oszlopot „Attitude” meg egy új soros felbontású. Ez határozza meg a minimális eleme „Attitude” oszlopban. A mi esetünkben ez az állásfoglalás sor 32. Minden bemutatott elemek piros betűkkel (lásd a 3. ábra). Ebben a következő iteráció vége a következő iteráció a változó x2 származik alapján (ez megmondja egy új megoldást a vonal), akkor helyébe egy változó x1 (ez megmondja az új engedélyezési oszlop), és minden számítás ismétlődnek újra.