A nem triviális valószínűségi feladatok
Röviden: „Találd meg az átlagos területe a vetülete a kocka éle hossz 1 síkra egy izotróp eloszlású vetület irányára.” Más szavakkal, mi az átlagos tervezett területen a kocka minden lehetséges orientációban?
Ez az üzenet feltárja a használata Mathematica, hogy megértsék, és végül a probléma megoldására. Ez újrateremti én megoldást erre a problémára.
A vetítés a négyzet egy egyenesen
Mielőtt a helyzet a doboz, azzal kezdtem, az egység területén, véletlenül megfordult a tömegközéppontja, azzal a szándékkal, hogy találjanak vetítés átlagos hossza a vízszintes tengely.
Az egyszerűség kedvéért, én helyeztük a tömegközéppontja a származási területen.
Megtaláltam a bal és jobb oldalán a vetítés, mint a legkisebb és a legnagyobb x koordináta a négyzet csúcsai körül forogva származási szög α:

Ezután egyesítjük ezeket a feladatokat a manipulálni [], hogy képes legyen dinamikusan változtatni a forgási szög:
Az lesz a vetített hossza függvényében a forgásszög:

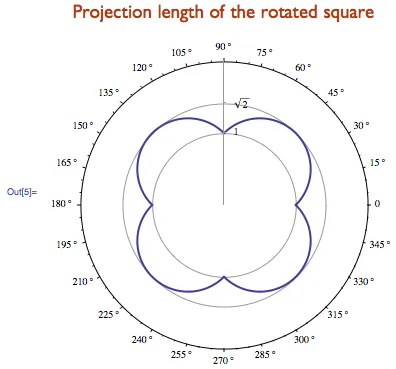
Feltételezve, hogy az elfordulási szög α egyenletesen oszlik el a 0 ≤ α