A prímszám vagy egy bizonyos ciklus Mathcad

A prímszám vagy ciklus jellemzőit MathCAD

Annak illusztrálására, a használata úgynevezett ciklus MathCAD típusú számtani sorozat (normál ciklus) levelet függvényt, amely meghatározza, hogy egy egyszerű, előre meghatározott n pozitív egész:

ellenőrizze a funkció egy egyszerű szám MathCAD

Ez azt feltételezi, hogy az átvitt k száma n - egyszerű (beállítja az R változó értéke 1), majd egymás után beolvassa a maradékok modulo n értéke 2, 3, ..., gyökér (n) - a maradékok modulo 1 és n ellenőrizze nincs értelme, és ha a szám nem elsődleges, sem annak két egész tényező nem lehet nagyobb, mint a négyzetgyökét (5 * 5 = 25 és 5 egyenlő a négyzetgyöke 25, és ez a szám, amelyre 25 lenne osztható egyenletesen nagyobb, mint 5, nem létezik) .

A fennmaradó osztás értéke n értéke i megtalálható a standard függvény MOD (N, i). Ha a talált legalább egy maradék nulla, Egyszerű függvény írja a visszaadott érték r = 0, és megszűnik a ciklus tesztek, különben r értéke egyenlő marad 1, mivel hozzá van rendelve a hurok.

Tesztelje funkció lehet, ha írsz egy másik funkció, amely egy vektor összes prímszám nem előre meghatározott értéknél nagyobb N:

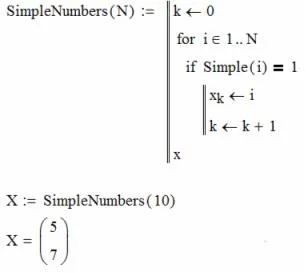
Minden prímszám nem haladja meg egy előre meghatározott N - megvalósítás MathCAD

Mint látható, a Simple hibás funkció - például, hogy nem veszi figyelembe az egyszerű számok a 2. és 3. A probléma az, hogy a ciklus kerül végrehajtásra, ha a kezdeti értéke a ciklus paraméter nagyobb, mint az utolsó pályán ciklus, és egyenlő az 1 (az alapértelmezett). Például, az n = 2 ciklus határa a padló (a gyökér (2)) = 1, és a ciklus ellenőrzi a maradékok modulo n = 2: 1 és 2 nullával egyenlő, meghatározza, hogy a 2-es szám - nem könnyű feladat.

Nem lenne helyes, hogy végre a belső hurok a while:

Minden prímszám nem haladja meg egy előre meghatározott N - megvalósítása révén, miközben

vagy kérjen hurok egyértelmű lépés egyenlő 1:

Minden prímszám nem haladja meg egy előre meghatározott N - megvalósítás MathCAD

Az utóbbi kiviteli alaknál, a 2. és 3. egy funkciója, hogy feldolgozza külön hibák elkerülése „Ez kell határozni egy változtatható tartományban az egymást követő értékeinek” - ebben az esetben fordul elő, ha az érték a padló (root (n)) kisebb, mint három.

A második érdekes pont - a klasszikus hurok MathCAD az, mint tudjuk, a jobb a jel általában fel ∈ diszkrét érv.

Azonban Mathcad lehetővé teszi, hogy hozzanak létre egy diszkrét változó a jogot a jel ∈ vektor vagy mátrix. Továbbá lehetőség van arra, hogy a lista vektorokat vagy mátrixok, vesszővel elválasztva. A skalár változót a bal oldalon a jel ∈ viszont elviszi az értékét minden egyes eleme az egyes nem skalár érték, a megadott sorrendben. A bemutatott képernyőkép mutatja, hogyan használja egy változó (k elemek és polc) algoritmikusan generált x vektor minden pozitív elemeit vektorok paraméterek A és B

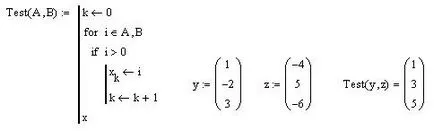
List vektorok a programciklust MathCAD