A rezgések amplitúdójának, az elmélet és az online kalkulátorok
Ismételt mozgások vagy vibráció nevezett folyamatokat.
Jellegétől függően a rezgések lehet mechanikus, elektromágneses, akusztikus, stb Más típusú oszcillációs leírt használatával ugyanazokat az egyenleteket, és így ugyanazt a jellemzőkkel.
Ingadozások az úgynevezett szabad (menjen a saját), ha ezek rovására történjen az energia, mely által termelt oszcilláló rendszer egyszer és további külső hatások a rendszerben nincs.
A legegyszerűbb fajta rezgések harmonikus rezgések.
Úgy hívják ezeket a rezgéseket harmonikus rezgések, amelyek egy oszcilláló nagysága időben változik szerint a szinusz vagy koszinusz ..
Hagyja, hogy a harmonikus rezgéseket egy paraméter $ s $, akkor ezek a rezgések leírható a következő egyenlet szerint:
ahol a $ A = s_ $ - oszcilláció amplitúdója; $ $ _0 - ciklusos (körkörös) oszcillációs frekvencia; $ \ Varphi $ - kezdeti fázis ingadozások (fázis $ t = 0 $); $ (_ 0t + \ varphi) $ - fázis ingadozások.
Úgynevezett maximális amplitúdója, amelynek értéke rezgések venni. Mivel a koszinusz (szinusz szerű) között mozog egy-mínusz egy, akkor a értéke $ s $ belül van $ -A \ le s \ le $ + A.
Módszer forgó vektor oszcillációs amplitúdóját
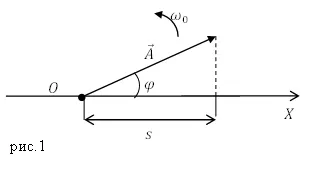
Harmonikus rezgések ábrázolható grafikusan (1. ábra), a használata vektor diagramok módszer (vagy egy olyan módszert a forgó vektor amplitúdó). Erre a célra, amelyekből - az önkényesen kiválasztott pont X tengely, ez az úgynevezett egy pont O, szögben egyenlő a kezdeti szakaszban (szög $ \ varphi $), késlelteti a vektor $ \ overline $. A hossza Ezt a vektort az amplitúdó ($ A $) oszcillációk. Ha ezt a vektort forgatjuk szögsebességgel $ $ _0, a vetülete a végén a vektor mozog az X tengelyen, és értéke legfeljebb $ -A $ $ A $, ahol a törvény az oszcilláló értékek lesznek, mint például az (1) egyenlet. Kiderült, hogy a harmonikus rezgéseket leírható útján vetítés tengelye vektor amplitúdója $ \ overline $, ami késik egy tetszőleges pont ezen a tengelyen szögben $ \ varphi $, forgatható szögsebességgel körül $ $ _0 kiválasztott ponthoz.
Példák problémák megoldás
Feladat. Anyag pont végez harmonikus rezgéseket, amely leírja az egyenlet: $ x = 0,1_0t + \ varphi) (m) \> $. Ismeretes, hogy az időszak oszcilláció e pont egyenlő T = 5 c. Mi az a sebesség az amplitúdó ($ v_m $) és a gyorsulás amplitúdó ($ a_m $) ezen a ponton?
Határozat. Először is, azt látjuk, a ciklikus rezgési frekvenciája pont, mint tudjuk az időszak oszcilláció:
Ismerve a variációs koordinátáit határozza meg, hogyan sebessége az anyag pont:
ahol $ x_m = 0,1 $ a feltétellel a probléma.
Egyenletből (1.2), hogy az amplitúdó a oszcilláció sebessége a lényeg:
A törvény a változás sebessége, megkapjuk a törvény változása gyorsulás pontot:
A törvény (1.3), hogy az amplitúdó a gyorsulás pont egyenlő:
Feladat. Vízszintes tavasszal, melynek rugalmassági együttható egyenlő $ k, $ csatolt labda tömege $ M $. A labda egy sima asztalra, amely felett súrlódás nélkül mozoghat. Bullet repül vízszintesen és megüti a labdát beszorul benne. kezdősebesség előtt a hatás $ v_0 $, golyó tömege $ m $, hatása sebesség irányított tengelyével párhuzamosan a tavasz. Mi a rezgések amplitúdójának a labdát a golyó? A tömeg a tavaszi és a közegellenállás elhanyagolható.
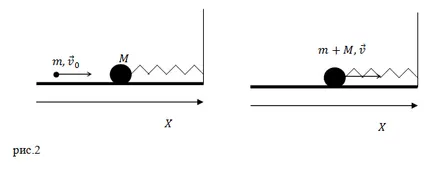
Határozat. Írunk a törvény lendületmegmaradás a rendszer labda - labda (ütni), és a labda a golyó közvetlenül az ütközés után:
A 2. ábrából kitűnik, hogy a (2.1) lehet átalakítani, hogy:
Tól (2.2) kifejezzük a labda sebességét után azonnal lövedék hatását:
Rendszer golyó labda, kiegyensúlyozatlan állapot golyó elérje. Ez teszi elérhetővé harmonikus rezgések. Kinetikus energia átalakul potenciális energia sűrített rugók. A két állam a rendszer (az első állam - a legnagyobb sebesség a rendszer mozgását, a második állapot maximális kompresszió a tavasz) összhangban a törvény az energiamegmaradás, írunk:
ahol a $ x_m $ - oszcilláció amplitúdója a labdát, egy golyó. Behelyettesítve fordulatszám-érték (2,3) a (2.4) és a kifejezett amplitúdó: