A szabadsági foka a szilárd - studopediya

Merev test kinematikai

Abszolút szilárd test úgynevezett anyagi test, geometriai alakja és méretei, amelyek nem változnak semmilyen mechanikai hatást gyakorol a részét más szervek, és a távolság közötti bármely két annak pontot állandó marad.

merev test kinematika, valamint a merev test dinamika, az egyik legnehezebb szakaszai során elméleti mechanika.

Merev test kinematika probléma ősszel két részből áll:

1. A mozgás feladata és meghatározása a kinematikus jellemzői a test mozgásának egészére;

2. A meghatározás a kinematikai paraméterek (pályája, a sebesség és a gyorsulás) mozgásának egyéni test pont.

Jelenleg öt fajta merev test mozgása:

1. transzlációs mozgást;

2. A forgatás körül rögzített tengely;

3. síkbeli mozgás;

4. A forgatás egy rögzített pont körül;

5. A szabad mozgás.

Az első két nevezik egyszerűen egy merev test mozgások:

Szilárd számú szabadsági fokkal a számos független paramétertől, amelyek egyértelműen meghatározzák testhelyzet viszonyított térben a figyelembe vett keretben.

merev test mozgása nagymértékben függ annak számú szabadsági fokkal.

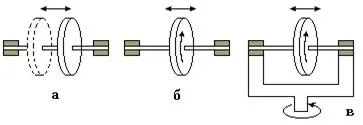
Vegyünk egy példát. Ha a lemez nem forog, csúszhatnak rögzített a tengelye a referencia rendszer (. Ábra), az, hogy ez a referenciakeret, nyilván, csak egy szabadságfokot - a lemez helyzetét egyedileg határozzuk meg, például az X-koordinátája a közepén, mentén mérve tengely. De ha vezetsz, továbbá szintén elforgatható (ábra b.) Ez lesz az egyik nagyobb fokú szabadságot - összehangolja x j hozzáadjuk a forgásszög tengelye körül a lemezt. Ha a tengely a lemez be van fogva egy keretben, amely foroghat egy függőleges tengely körül (. Ábrán), a száma szabadsági fokkal egyenlő három - j x, és a forgatási szöget adunk az F keret.

Szabad tömege térbeli pontban három szabadsági fok: mint például a Descartes koordinátái x, y és z. Pontok koordinátáinak is meghatározható a hengeres (R, j, z) és gömb alakú (R, j, f) referencia rendszerek, de a paraméterek száma, amely egyedileg meghatározza a helyzetét egy térbeli pontban mindig három.

Az anyagi pont a síkon két szabadsági fok. Ha a sík XOY válasszon egy koordináta-rendszer, a X és Y koordináták határozzák meg a pont pozícióját a gépen, és a z koordináta azonosan nulla.

Szabad anyagi pont a felületen bármilyen két szabadsági fok. Például: a helyzet a Föld felszíne által meghatározott két paramétert: a hosszúsági és szélességi fokok.

Anyagi pont a görbe semmiféle van egy bizonyos fokú szabadságot. Paraméter helyzetének meghatározására egy pontot a görbe lehet, például, a távolság a görbe mentén a származási.

Tekintsünk két anyagot tér pontjait, csatlakozik egy merev rúd hossza l. A helyzet az egyes pontok három paraméter határozza meg, de a kapcsolatuk kiszabni.

Az egyenlet egy egyenlet kommunikáció. Ebből az egyenletből, hogy az egyik koordináta lehet kifejezni a fennmaradó öt koordináták (öt független paraméterek). Ezért ez a két pont () öt szabadsági fokkal.

Nézzünk három lényeges ponton a térben, nem fekszenek egy egyenes vonal, amelyeket három merev rúd. A több szabadsági fokkal Ezeknek a pontoknak egyenlő () hat.

Szabad merev test általában hat szabadságfok. Sőt, a helyzet a test a térben képest a vonatkoztatási rendszer határozza meg, megadva a három pontot, hogy nem fekszenek egy egyenes vonal, és a két pont közötti távolság szilárd változatlan marad minden mozdulatát. A fentiek értelmében, a fokok száma szabadság egyenlőnek kell lennie hat.