A számos különböző k-részhalmazát elemi n-általános készletek - studopediya

Nézzük, mint ahány különböző részeiben k halmaz elemeit tartalmazó n elemek (k <п).

TeoremaChislo különböző K-n-elemű halmaz részhalmazainak egyenlő az elemi

ha a csökkentés n! = N * (n - 1) *. * 3 * 1 * 2 faktoriális hívott szám n (n-olvasható faktoriális). 0! = 1. A csökkentés.

Bizonyítás. A konstrukció egy k elemű részhalmaza A, szükség van (k - 1) -element szett csatlakozni egy n - k + 1 elemek, amelyek nem szerepelnek ezen alcsoportjában. Mivel a számát (k - 1) -element részhalmazát az azonos, és az egyes részhalmazokban lehet k elemű n - k + 1 módon, az alapvető szabályt a kombinatorikus szám-Toriki kap * (n - k + 1) részhalmazát. Azonban nem minden ilyen alcsoportok eltérő, mivel minden k olyan elemi részhalmaza is építeni k módon. ezért

Mivel - száma Singleton részhalmazok A - egyenlő n, akkor

Tetszőleges k elemű részhalmaza A nevezik kombinációja, vagy a minta, és a szám - a kombinációk száma, illetve kombinációi n elem k elemek.

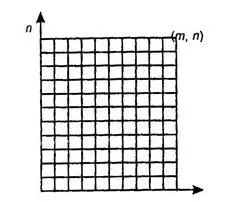
Binomiális együtthatók egy érdekes geometriai Interprom-tatsiyu. Engedje meg, hogy egy téglalap alakú sakktábla mérete m n, time-elmozdulások koordinátarendszerben. Ez a tábla áll m * n általános négyzetek elválasztva n - 1 Hori-tal vonal és m - 1 függőleges. Határozza meg, hogy hány különböző legrövidebb utak érhető el az a pont (0, 0) az a pont (m. N) ezen a fórumon.

Minden legrövidebb út vezet a pont (0, 0), hogy a pont (m, n), nyilvánvalóan áll m + n oldalú elemi terek, amelyek közül m Hori-zontally és n függőleges. Ezek az utak különböznek csak 1 számú vízszintes és függőleges oldalai. Ennélfogva, az összes utak egyenlő a számos módon, amelyek a m ​​+ n felek kiválaszthatja n-ver-helyi, azaz ez a szám.

Megjegyezzük, hogy az ember nem számíthat a függőleges oldalai,

valamint a horizontális. Ez azt jelenti, van egy fajta a legrövidebb útvonalat, és ennek következtében az egyenlőség:

Ez az egyenlőség az úgynevezett „formula a szimmetria.”

Ebből a képletből van az eredménye:

amelynek a címe „hozzáadásával képlet”. Megmutatjuk, ezt a hatást.

Az egyesített csapat egyetemi röplabda foglalkoztat 15 fő. Hány különböző lehetőségeket kell vizsgálni az edző a meccs előtt, hogy be a játékosok listáján a játékban?

Megoldás: A játékosok száma a röplabda csapat hat. Ennélfogva, a szám minden lehetséges opciókat - számos különböző alcsoportok, amely hat elemek egy sor tizenöt elemek. Így, 2. tétel van