A változás sebessége függvényében

Home | Rólunk | visszacsatolás

Meghatározása differenciálhányados keresztül limit

Tegyük fel, hogy a szomszédságában a függvény definiált differenciálhányados a határpont, ha létezik,

Hagyományos kijelölése differenciálhányados egy ponton

A függvény deriváltját ponton. hogy a határ, nem létezik, vagy létezik, és lehet véges vagy végtelen. A függvény differenciálható egy olyan ponton, ha, és csak akkor, ha a származék ezen a ponton létezik és véges:

Mert differenciálható függvények a közelben egyenlő képviselet

Megjegyzések nevezzük növekmény az érvelés, és a növekmény a függvény értékét az időpontban

· Legyen a függvény véges származék minden időpontban differenciálhányados

· Egy függvény, amely egy származéka egy olyan ponton, hogy folyamatos. Ennek a fordítottja nem mindig igaz.

· Ha a derivált függvény maga folytonos, akkor a függvény az úgynevezett folytonosan differenciálható és írd be:

Geometriai és fizikai jelentése a származék

A lejtőn az érintő

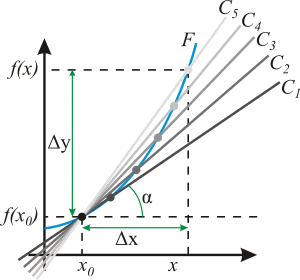
Geometriai értelmében a származék. A grafikonon az X0 választjuk abszcissza és ordináta megfelelő a kiszámított F (x0). A közelben tochkix0 kiválasztott tetszőleges x pont. Keresztül a megfelelő keresztirányú (az első C5 világosszürke vonal) a függvény grafikonját F tartják pont. távolság # 916; x = x - x0 nullához, így a szekáns halad érintője (fokozatosan sötétedő vonal C5 - C1). A szög tangense # 945; a lejtőn a tangens - a származékot a ponton x0.

Ha a függvény véges származékot egy pont a környezetében lehet közelíthető egy lineáris függvény

A funkció az úgynevezett pontját érintő szám egy lejtőn, vagy a szög tangense naklonakasatelnoy vonalat.

A változás sebessége függvényében

Hagyja, - a törvény egyenes vonalú mozgás. Akkor ez fejezi ki a pillanatnyi sebességét, amikor a második derivált kifejezi a pillanatnyi gyorsulás idején

Általában, a származékot a ponton kifejezi a változási sebességének a függvény. azaz az áramlási sebesség a folyamat leírt függőség

Származékai magasabb rendű

A koncepció a származék bármilyen sorrendben definiáljuk rekurzívan. Hisszük

Ha egy differenciálható függvény. Az elsőrendű származékot adják

Tegyük fel most, hogy a származékot sorrendben van meghatározva egy pontjának szomszédságában és differenciálható. majd

Ha a funkció egy bizonyos tartományban D parciális deriváltja változók közül az egyik, az úgynevezett származékot, maga is függvénye lehet, hogy egy bizonyos ponton a részleges származékok ugyanazon vagy bármely más változó. Az eredeti funkciója ezek a származékok a részleges származékok a másodrendű (vagy második részleges származékok).

A parciális deriváltja a másodrendű vagy magasabb, vett különböző változók az úgynevezett vegyes parciális derivált. Például,

A művelet a megállapítás a származékos hívják differenciálás. E művelet során gyakran dolgozik saját, összeg, termék jellemzői, valamint a „funkcióit funkciók”, azaz kifinomult jellegét. Ennek alapján a származékos ügylet definíciójának, akkor következtetni lehet a szabályokat a differenciálás, hogy megkönnyítse ezt a munkát. Ha C - állandó, és F = f (x), g = g (x) - néhány differenciálható függvények, majd a következő szabályokat differenciálódás:

• Ha a funkció adott parametrikusan:

· Képlet származékos művek, és a kapcsolatok is általánosítható az esetben az N-szeres differenciálódás (Leibniz képlet):

ahol - binomiális együtthatók.