A vektorok és mátrixok
Vektorok és mátrixok.
Egy rendezett sorozata a valós számok a1, a2, .... Akkor kötődni egy társított fogalom vektor n-dimenziós tér és a kijelölt, mint:
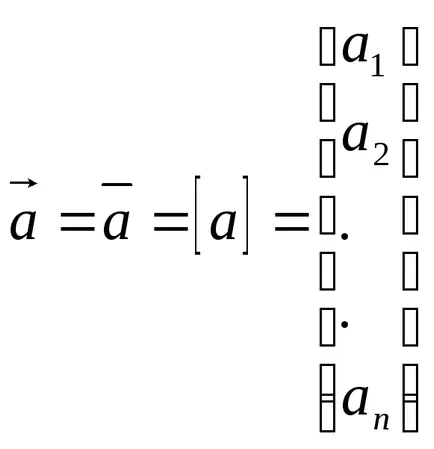
Típusai és jellemzői vektorok.
Nulla vektor - vektor, amelynek minden komponens nulla.
Az egység vektor - vektor hossza egyenlő egy:
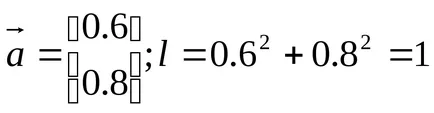
Transzponált vektor - egy vektor, amelynek komponensek el vannak rendezve egy sorban:
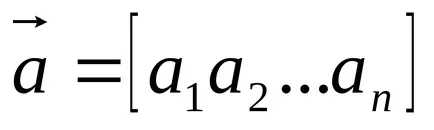
Két vektor azonos méretű egyenlő, ha azok a megfelelő komponensek:
A számok halmaza elrendezett négyszögletes tömb, ami n sorból és m oszlopból, az úgynevezett mátrix és jelöljük:
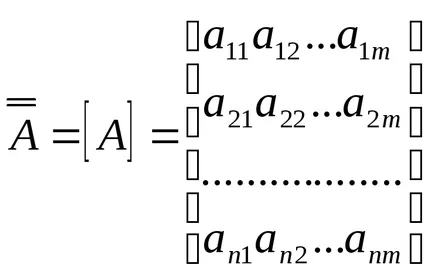
A helyzet az elem

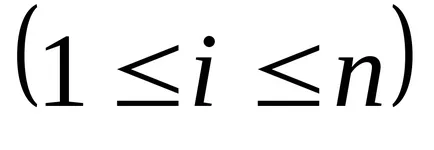
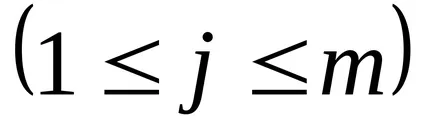
Vektor vonal - álló mátrixot egy sorban n = 1
Oszlop vektor - mátrix, amely egy oszlop m = 1
Egy négyzetes mátrix - mátrix, ahol n = m
Felső háromszög - mátrix, amelynek
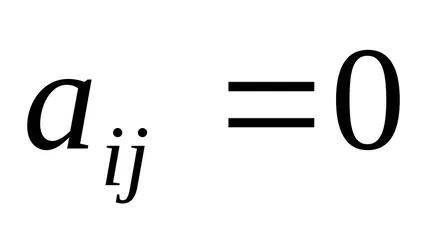
Alsó háromszög - mátrix, amelynek
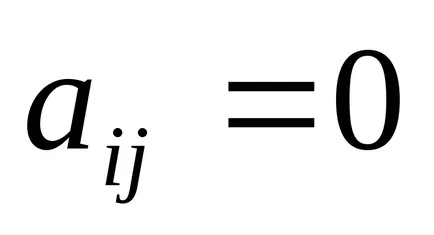
Átlós - mátrix, amelynek
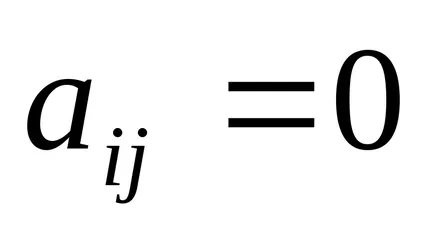
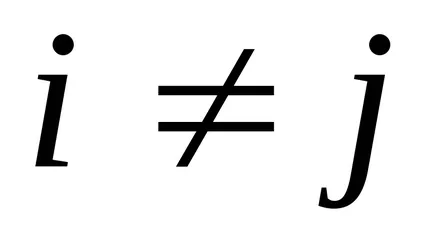
Identity - mátrix, amelynek
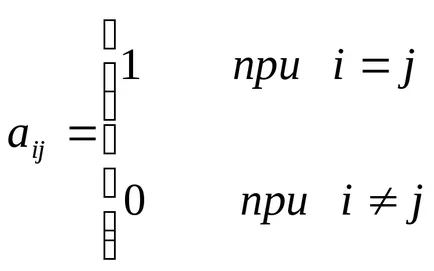
egyenlőség mátrixok
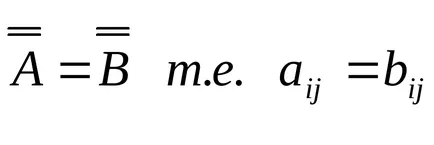
Jellemzők és működését.
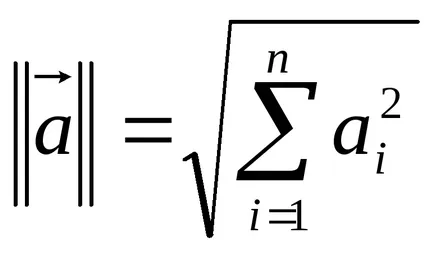
A norma a mátrix (euklideszi).
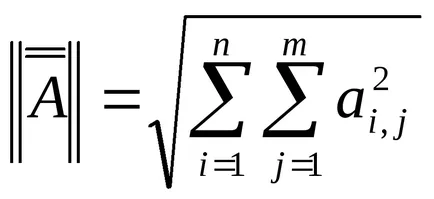
Összeadás és kivonás, vektorok.
Összeadni és kivonni csak a vektor azonos méretű. Az összeadás eredménye (kivonás) egy vektor, amelynek az összetevői az összegével egyenlő (különbség) a megfelelő komponensek két más vektorok.
Összeadás és kivonás mátrixok.
Összeadni és kivonni csak a mátrix azonos dimenzióban. Az összeadás eredménye (kivonás) olyan mátrix, amelynek elemei az összegével egyenlő (különbség) a megfelelő elemek a másik két mátrix.
Az ingatlan hozzáadás (kivonás) mátrixok:
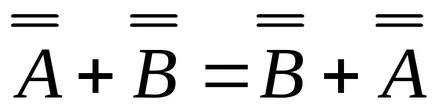
Szorzás egy vektor egy konstans.
Az a szorzás eredményét egy vektor, amelynek az összetevői egyenlő a termék a megfelelő komponenseket a bemeneti vektor egy konstans.
Szorzás egy mátrix egy konstans.
Az eredmény a szorzás olyan mátrix, amelynek elemei egyenlő a termék a megfelelő elemek az eredeti mátrix egy konstans.
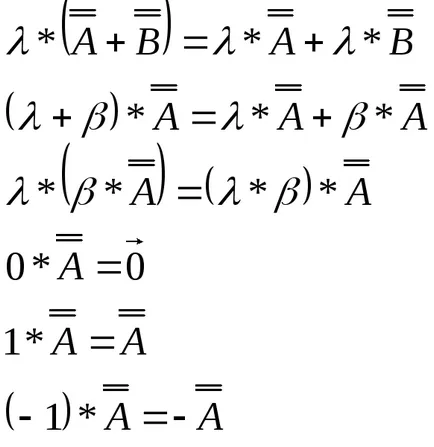
Transzponált mátrixszal - helyettesíti a sorok, az oszlopok, azaz
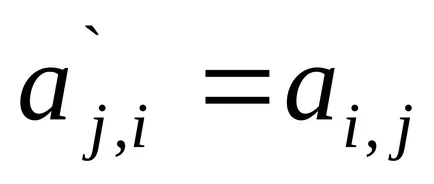
Oszlopainak száma A mátrix egyenlőnek kell lennie a sorok számát a mátrix B.