A vetítés a vektor a tengelyen

Projection vektor. feküdt a tengelyen. Ezen a tengelyen a szám abszolút értékét a vektor hosszának és együttesen a „+” jel, ha az irányt a vektor egybeesik a tengely irányában, és a „-” jel, ha ellenzik.

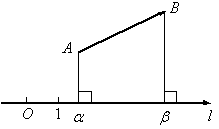
Tegyük fel, hogy nincs rajta a tengelyen, akkor képpont A és B elhagyható merőlegesek a tengelyre: pontokat szerzett. A vektor az úgynevezett komponens vektor tengelye mentén L.

Projection vektor. nem feküdt a tengelyen. Ezen a tengelyen az úgynevezett vetülete komponense a vízszintes tengelyen.

stb L - vetülete a vektor a tengelyen L.

- bővítése a vektor komponenseit, valamint a koordináta-tengely.

- vektor hossza, kifejezve a koordinátáit.

A sugár vektor - vektor, az elején, amely a származási. Azt koordinátákat.

Szög mezhdui tengely L jelentése a legkisebb szög irányát és a pozitív tengely irányában L.

Tétel: vetítési vektorba visszük tengelye hossza egyenlő a terméket vektor a koszinusz az a köztük lévő szög.

A iránykoszinuszokat - koszinuszok a szögeket, hogy a vektor teszi a koordináta-tengely.

Tétel. vetülete vektor összege a tengely az összege a nyúlványok ezen vektorok ezen a tengelyen.

Tétel: A két pont közötti távolság egyenlő a négyzetgyöke négyzetösszege a különbségek a megfelelő koordinátákat.

Tétel: vektorana megszorozzuk száma annak vetülete L megszorozzuk továbbá L.

Tétel a két vektor egyenlő, szükséges és elégséges az, hogy kiemelkedések bármely tengely volt egyenlő.

Lineáris függés és függetlenség vektorok. alapként

Legyen n-vektor és a n-konstans c1, c2, ... .sn.

Vektor nevezik lineynozavisimymi:

1) Ha vannak c1, c2, ... .sn. amelyek közül legalább az egyik nem nulla, hogy a lineáris kombináció egyenlő nullával.

2) ha a legalább egy vektor a rendszer lehet kifejezni, mint egy lineáris kombinációja a többiek.

Vektor nevezik lineynonezavisimymi:

1) ha a lineáris kombináció nullával egyenlő, ha, és csak akkor, ha c1 = c2 = ... = cn = 0.

2) Ha a fenti vektorok képviseletében a lineáris kombinációi a többiek.

Három nulla vektor nevezett síkban vannak. ha azok az azonos vagy párhuzamos síkokban.

Alapon a síkban és a térben

A gyűjtemény a két lineynonezavisimyh vektorok tartozó ezen sík nevezzük alapján ezen a síkon.

NB! Bármilyen vektor fekvő ebben a síkban lehet kifejezni a két vektor.

A gyűjtemény a három lineynonezavisimyh vektorok nevezzük alapján a teret.

Basis a térben, amelynek vektorok kölcsönösen merőleges, és a hossza, amely egyenlő egy, az úgynevezett ortonormált.

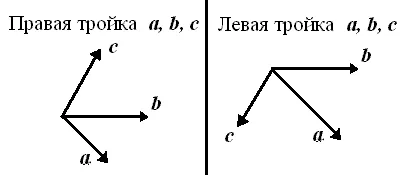
Triple vektorok hívják a jobb oldalon. ha a vége felől nézzük a legrövidebb vektort a forgás az óramutató járásával ellentétes.

Trojka nevű vektorok maradt. Ha nézve a végén a legrövidebb vektort a forgás bekövetkezik az óramutató járásával megegyező irányba.

Descartes-alapon. A hossza a derékszögű vektor alapján

Egy derékszögű koordináta-rendszert egy által képezett tér három, egymásra kölcsönösen merőleges koordinátatengelyeken OX, OY és OZ. A tengelyek metszik az O pont, amely az úgynevezett származási, mindegyik tengely egy pozitív irányba, nyilakkal jelzett, és egység-intervallumokkal, a tengelyekre. Egységek általában megegyezik az összes tengely (amely nem kötelező). OX - x-tengely. OY - az y-tengelyen. OZ - a Z-tengely.

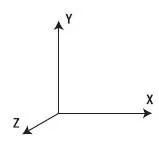
- hossza a vektor kifejezve a koordinátáit

Skalárszorzat. Expression skalárszorzat a koordinátákat. A fizikai értelemben skalárszorzat

Skaláris termék és ez a szám egyenlő a termék hosszának ezen vektorok által koszinusza a köztük lévő szög.

A tulajdonságok a skalár termék:

Tétel két nem nulla vektorok ortogonális (merőleges) akkor és csak akkor, ha azok skalár szorzat nulla.

Expression skalárszorzat a koordináták