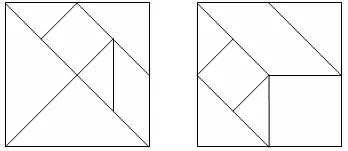
Ábrákon a négyzet alakú darabot

Home | Rólunk | visszacsatolás
Között a hasznos és szórakoztató szórakoztató tárgya ábrákon hét négyzet alakú darabot, vágott 3. ábra szerinti (a), ahol a készítmény mind a hét bitet kell használni adott formában, és meg kell sovány akár részlegesen, egymásra.
Ábra. A 4. ábra a szimmetrikus számok [1]. Próbálja felvenni ezeket a formákat a részek a tér ábrán látható. 3 (a).
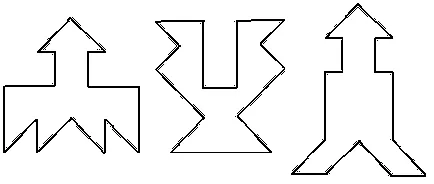
Ezekből rajzok lehet hajtani, és sok más alakok (például, a képek a különböző tárgyak, állatok, stb).
Kevésbé gyakori lehetőség az, hogy a játék darabjai a darab négyzet ábrán látható. 3, (b).
Magic square «n 2, a tér” nevezzük egy négyzet osztva 2 n megtöltött cella az első n 2 pozitív egész szám úgy, hogy a számok összege minden vízszintes vagy függőleges sorban, valamint bármely az átlók a tér azonos szám
Ha csak az azonos mennyiségű számok állva vagy vízszintes, vagy függőleges sorban, a tér nevezik semimagic.
Magical április 2 jelentése elnevezett téren Dürer, matematikus és előadó XVIveka ábrázoló téren a híres festmény „Melankólia”.
By the way, a két alacsonyabb az átlagos négyzetes forma száma 1514-időpontjától létre a festmény.
Már csak nyolc devyatikletochnyh mágikus négyzetek. Ezek közül kettő tükörképei egymásnak, az ábrán látható; A többi hat lehet ezekből négyzetek középpontja körül forgatás 90 °, 180 °, 270 °
2. Ez könnyen teljesen vizsgálja a mágikus négyzetek az n = 3
Valóban, S3 = 15, és már csak nyolc módon, hogy képviselje a szám 15 összegeként a különböző számokat (egytől kilencig):
Megjegyezzük, hogy minden egyes számhoz 1, 3, 7, 9 tartalmazza a két, és az egyes számok 2, 4, 6, 8 - a három fenti összegek, és csak a szám 5 a négy összegeket. Másrészt, nyolc trehkletochnyh sorozat: három vízszintes, három függőleges és két átlós - mind a sarkában egy négyzet sejt áthalad a három közepén keresztül négyzet négy, és az egyes, a másik két sorban a sejtek. Következésképpen, a számot 5 szükségszerűen állni a központi sejtszám 2, 4, 6, 8 - a szögletes sejtekben, mint az 1, 3, 7, 9 - a fennmaradó téren sejtek.
Ha annak érdekében, hogy rendezni ezeket a tényezőket, hogy minden „lépés”
találkozik szorzók több prímszám; számuk
egyébként. de ezek a tényezők sorolhatók. - és ebbe
Következésképpen a számos tényező az egyenletben a szorzó, amely magában foglalja a pontosan egy, kettő, három, stb szeres, illetve egyenlő a szám:
2. Ez könnyen teljesen vizsgálja a mágikus négyzetek n = 3. Valóban, S3 = 15, és már csak nyolc módon, hogy képviselje a szám 15 összegeként különböző számú (egytől kilencig):
Megjegyezzük, hogy minden egyes számhoz 1, 3, 7, 9 tartalmazza a két, és az egyes számok 2, 4, 6, 8 a három fenti összegek, és csak a szám 5 a négy összegeket. Másrészt, nyolc trehkletochnyh sorozat: három vízszintes, három függőleges és két átlós - mind a sarkában egy négyzet sejt áthalad a három közepén keresztül négyzet négy, és az egyes, a másik két sorban a sejtek. Következésképpen, a számot 5 szükségszerűen állni a központi sejtszám 2, 4, 6, 8 - a szögletes sejtekben, és az 1, 3, 7,9 - a fennmaradó téren sejtek.