Az alapvető tulajdonságai hatványsorok - studopediya
1) Az összes pontot fekvő intervallumon belül a konvergencia, az energia mennyisége sorozat folytonos függvény az x változó:
2) A hatványsor Terminusonként lehet integrálni az intervallumon belül a konvergencia:
3) hatványsor Terminusonként megkülönböztethetünk belső konvergencia intervallum:
Amikor termwise integráló és differenciáló hatványsor intervallumok konvergencia nem változik.
4. példa Keresse meg az összeget a sorozat
Határozat. Először azt látjuk, az intervallum a konvergencia a sorozat n
Következésképpen, számos konvergencia intervallum (-1, +1). Differenciáló (3,6), van
S ¢ (x) = 1 + x + x 2 +. + X n +.
A jobb oldali ez a kifejezés - a geometriai sorozat q = x, amely konvergál az ½x½<1. Поэтому, используя формулу суммы сходящейся геометрической прогрессии, получим
Ezért az összeget az eredeti sorozat fogja találni az integráció
Azt találjuk, C. tól (5.6) következik, hogy S (0) = 0. Következésképpen,
0 = - ln (1-0) + C, C = 0.
Ezért, S (x) = - ln (1-x) =.
Együtt hatványsorok képest a változó x gyakran tekintik a változó teljesítmény sorozat (X-a), azaz sorozat formájában
Nyilvánvalóan ez a szám helyettesítve y = (x - a) alakítjuk át egy sorozat típusú (3.3). Ezért, ha a teljesítmény sorozat (3.3) az az időköz a konvergencia - R Taylor-sor. Tegyük fel, hogy az f (x) x = a van-származékok bármilyen sorrendben. Tegyük fel, hogy van egy konvergens hatványsor a0 + a1 (X-a) + A2 (X-a) 2 +. AN + (X-a) n +. = (3.8) amelynek összege egyenlő az f (x). azaz Az együtthatók ezt a sorozatot. Nyilvánvaló, f (a) = A0. Differenciálás (3,8) x = a. van a1 = f ¢ (a). Differenciálás (3,8) x = a kettős kapjuk a2 = (f ¢¢ (a)) / 2. Folytatva a levezetése (3.8) láthatjuk, hogy számos tényező (kerülnek az alábbi képlet szerint Teljesítmény sorozat formájában nazyvaetsyaryadom Taylor f (x). Abban a különleges esetben a = 0 adja a Taylor-sor és ez az úgynevezett Maclaurin sorozat. 5. példa egy Taylor-sor f (x) = e x. Határozat. Mivel e x = (e x) ¢ = (e x) ¢¢ =. (E x) n. Ezután az x = 0 f (x) = e X f (0) = 1; f ¢ (0) = 1; f ¢¢ (0) = 1;. ; f (n) (0) = 1;. Következésképpen, Maclaurin függvény az y = e x a formája Series (3.11) konvergál a teljes tengely az y = e x. 6. példa elbontására Maclaurin f (x) = sinx. Határozat. Az f (x) = sin x, van: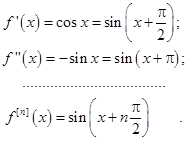
Ennélfogva, a Maclaurin sorozat sin x:
Hasonlóképpen, megkapjuk egy expanziós a funkció cos x:
Hasonlóképpen, akkor kap egy Taylor sorfejtés vagy Maklorenai sok más funkció.