Az egyenletek megoldása paraméterekkel
2. lecke másodfokú egyenletek paraméterekkel
3. lecke egyenletek paramétereinek meg kell oldani a Wyeth-tétel
4. lecke problémák megoldása paraméterekkel. Extrém.
5. lecke problémák megoldása paraméterekkel. Funkciót.
6. lecke megoldása egyenlőtlenségek paraméterekkel
7. lecke megoldása egyenletek paramétereinek
8. lecke rendszerek és egyenlőtlenségek
10. lecke egyenletek paraméterekkel és a modul
11. lecke exponenciális egyenlet egy paraméter
12. lecke trigonometrikus egyenletek paraméterként
13. lecke Vissza paraméter egyenlet
14. lecke Az egyenlet megoldása a paramétert a származékot.
15. lecke grafikus egyenletek megoldása egy paraméterrel.
16. lecke irracionális egyenlőtlenség paraméterrel.
17. lecke A megoldás a modul és a paramétert a geometriai értelmezést.
18. lecke A szükségesség elve és elégséges a problémák megoldásában a megfelelő paraméterekkel.
19. lecke A döntés racionális egyenlőtlenségek paraméter.
20. lecke Az egyenlet megoldása egy paraméterrel tartalmazó a gyökér
Lecke Focus: lineáris egyenletek paramétereit.
Egyenletek, amely továbbá az ismeretlen, és még literálértékeket nevezzük egyenletek paramétereit. Matematikai szerkezete (egyenlet egyenlőtlenség rendszer, több) tartalmazó, amellett, hogy a ismeretlen, és több alfabetikus értékeket hívjuk szerkezet paramétereket. Például egyenlet AX = b egy egyszerű lineáris egyenlet, és attól függően, az arány a és b együtthatók vannak a három lehetséges eset: ha egy nulla, és b értéke nulla, és ha nem egyenlő nullával, és ha a jelentése nulla, és b értéke nem nulla. Ez általában úgy két produkció a paramétereket a problémát. Az első stádium. Minden lehetséges értéke a paraméter vagy paraméterek, hogy megtalálja az összes megoldás előre meghatározott matematikai struktúra, például, hogy megoldja a egyenlőtlenség Hvostov 2 <1. Вторая постановка. Найти все значения параметра или параметров, при каждом из которых решение математической структуры удовлетворяет заданным условиям, например, найти все значения параметра а при которых система уравнений не имеет решений.
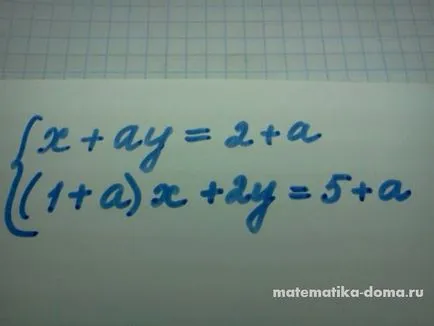
A komplexitás megoldása matematikai struktúrák paraméterekkel, hogy a változás a paraméter megváltoztatható nemcsak az együtthatók a struktúrák, hanem ODZ és típusok, módszerek és megoldások technikákat.
Lineáris egyenletek paraméterei
Lineáris egyenletek írásos általános formában, akkor tekinthető, mint egy egyenlet paraméterekkel, például ah = b, ahol x - ismeretlen, és, b ez, az úgynevezett paraméterek. Általában bármely egyenlet egy adott paramétert vagy referenciaérték az, amelyen eltűnik egy ismeretlen tényező.
Megoldásában a lineáris egyenlet a figyelembe vett paraméter az esetekben, amikor a paraméter néhány konkrét értékét az egyes egyenletek és azokat, amelyek különböznek tőle.
Egy különösen paraméter értékét, és jellemzően az értéke egy = 0.
Tekintsük a megoldás a következő egyenletek.
1. egyenlet megoldásához ax = b.

2. egyenlet megoldásához 2a (a-2) X = a-2



Tekintsük néhány példát



Mi megoldjuk az egyenletrendszert a fent említett.


Feladatok a független döntést.
1. feladat.
Mert milyen értékeket a paraméterek és az egyenlet ax = = 12 és 3 azonos gyökerek?
Find az érték, amelynél a gyökere a 3. egyenlet (x-4) -5 (x + 2) = Cj-6 az a szám 6?
, Amelyeknek az értékei és az egyenlet 5x-3a = 2-nek
- pozitív gyöke
- negatív gyök
- A gyökér több mint 10
- gyökér tartozó intervallum (1; 2).
Megjegyzés: A részletes megoldásokat ezekre egyenletek paramétereit láthatjuk a második leckét.