Az eloszlás a diszkrét valószínűségi változó

Egy korábbi feljegyzések azt jelzi, hogy a vizsgálat eredménye lehet egy numerikus változót. Másfelől, a numerikus változók vannak osztva diszkrét és folytonos. Diszkrét változók jellemző transzferek és számolás és folyamatos - a mérésre. Ebben és a következő néhány cikket fogja vizsgálni az általános helyzetet, és a legelterjedtebb elosztó, amely leírja a diszkrét véletlen változó. [1]

Megoszlása ​​diszkrét véletlen változó - ez egy teljes listát az összes lehetséges értékek egy véletlenszerű változó, ahol minden eredmény szállítjuk megfelelt annak a valószínűsége. Például, ábrán. Az 1. ábra a számának eloszlása ​​a jelzáloghitelek kiadott egy héten belül a helyi szervezete a bank. Ahogy a táblázat megmutatja az összes lehetséges kimenetelt, az összeget a valószínűségek 1.

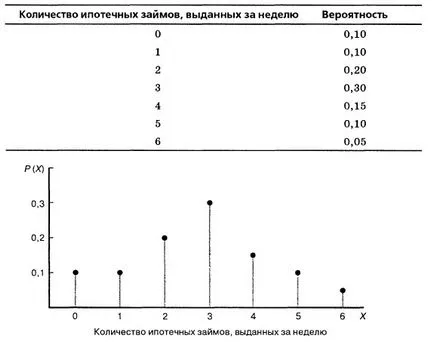
Ábra. 1. számának megoszlása ​​a jelzáloghitelek kiadott egy héten

Elvárás μ diszkrét véletlen velichinyX úgynevezett átlagos értéke a terjesztésre. Ez az érték az az összeg, a termékek valamennyi értékei az X valószínűségi változó a megfelelő valószínűsége P (X). Más szóval, a várakozás egy diszkrét véletlen változó X - súlyozott átlaga az összes lehetséges kimenetelt, ahol a súlyok a valószínűségek minden eredmény.

ahol Xi - i -e különálló értékét a véletlen X változó F (Xi) - i -ro valószínűségi értékek a diszkrét véletlen változó X.

A várható száma a jelzáloghitelek kiadott ezen a héten:
p = 0x0,01 + 1 × 0,1 + 2 × 0,2 + 3 × 0,3 + 3 × 0,15 + 5 × 0,1 + 6 × 0,05 = 0 + 0,1 + 0, 4 + 0,9 + 0,6 + 0,5 + 0,3 = 2,8

Megjegyzés: a várható száma a jelzáloghitelek kiadott ezen a héten fejezték ki számot, amely nem rendelkezik a szó szoros értelmében, hiszen a hitelek mérhető csak egész számok.

Dispersiyaσ két diszkrét véletlen X változó súlyozott átlaga négyzetes különbségek közötti összes lehetséges értékek és várakozás. A súlyok a valószínűségek a megfelelő eredmények:

ahol Xi - i -e különálló értékét a véletlen X változó F (Xi) - i -edik valószínűségi értékek a diszkrét véletlen változó X.

A standard deviáció σ egy diszkrét véletlen változó:

Az Excel kiszámításához leíró statisztika diszkrét valószínűségi változók szabványos funkciók, azonban általánosan használnak további oszlopokat közbenső számítások szerint olyan (1), (2) és (3), lásd. Ábra. 2. Az egyetlen kivétel - a várakozás - lehetőség van annak meghatározására, azonnal (nincs közbenső számítások) segítségével = SUMPRODUCT ().

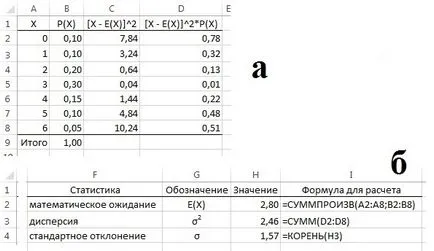
Ábra. 2. Az egymást követő kiszámítása leíró statisztika diszkrét valószínűségi változók: (a) bemeneti adatok és a közbenső számítások; (B) A végső számítások

Lehetőség van, hogy lemondunk a közbenső számítások. Ehhez használja a képletek array (ábra. 3. Lásd még a megfelelő lapot csatolt Excel-fájl). Ha nem használja az ilyen képletek korábban, ajánlom kezdeni olvasni Excel. Bevezetés általános képletű tömb. Érdekes, hogy néhány szabványos Excel funkciók már a tömbképletet, bár csak kevés. Különösen, fent használt SUMPRODUCT = ().

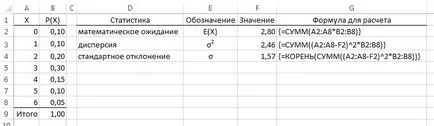
Ábra. 3. számítása leíró statisztika diszkrét valószínűségi változók segítségével egy sor képletek

Megjegyezzük, hogy a tisztasága a kísérlet, lehetséges, hogy nem hivatkozás nélkül egy köztes érték E (X) (mint referencia cella F2 a képletek kiszámításához használt σ 2 és σ, cm. G3 és G4 sejt ábrán. 3.). Ebben az esetben például, kiszámításához σ 2 kissé nehézkesebb képlet.