Az integrált vonópontra - studopediya
Tétel mintegy kiálló a derékszög.
Ha az egyik lábát a derékszög van síkjával párhuzamos projekció, és a második nem foglal egy kiálló helyzet (nem síkjára merőleges a vetítés), majd a megfelelő szögben a gépen vetítési várhatóan torzítás nélkül.
A fenti számok nevezzük odnokartinnymi. A fenti vetítési módszer lehetővé teszi, hogy egyedi módon oldja meg a közvetlen probléma -, hogy össze egy nyúlvány (rajz) geometriai képet.
Az inverz probléma ábrázoló geometria - a geometriai kép rajz Visszaépítés - megoldódott kétértelmű (több vagy számtalan megoldás). Ebből az következik, hogy a rajz nem odnokartinny az a tulajdonsága reverzibilitási. Projection rajz válik váltvaforgató hozzáadásával további információkat.
A mi természetesen fogjuk alkalmazni megfordítható rajz, amely az úgynevezett komplex rajz merőleges vetülete (KC)
Chertezhomnazyvaetsya rajz komplex, amely két vagy több összekapcsolt merőleges vetülete képalkotó geometriai képet.
Az elv az oktatás: geometriai vetített kép ortogonálisán legalább két egymásra merőleges síkban a nyúlványok, amelyeket azután megfelelően kombinálhatók egy síkban.
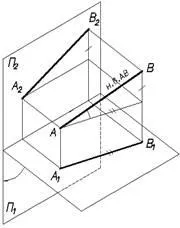
Point - nolmerny geometriai kép;
Szimbólumok pont - A, B, C, D ... 1,2,3 ... stb.;
P 2 (XOZ) - függőleges (elöl) a vetítési sík;
6. ábra A 6. ábra egy rajz odnokartinnym.
A rajz látható. 7 nevezzük pont összetett rajz.
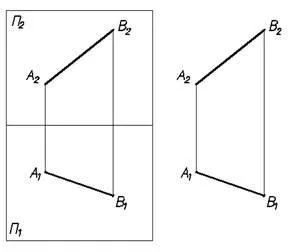
Mindkét ábra (6. ábra és a 7. ábra) egy grafikus ábrázolása a merőleges vetülete az azonos pont a két egymásra merőleges síkban (P1 és P2).
Ha KC Adott két előrejelzések a pont, azt mondhatjuk, hogy a pont egyedileg meghatározni KC