Bezier görbék (képletek és konstrukciós elvei) - studopediya
1. alapelvei Bezier görbék
1.1. Tulajdonságai Bezier görbéket
1.2. Kanonikus alakban Bezier görbét
1.3. Változó alakja a görbe
1.4. Vegyület több ágazatban
2. típusai GCP
3. Történelem görbék * (További vizsgálat)
Bezier görbe (képletek és konstrukciós elvei)
Általában a Bezier görbe - ebben a konkrét esetben - spline [1] (NURBS-görbe), amely úgy definiálható, mint egy súlyozott összege n + 1 ellenőrzési pontok, ahol a súlyok a Bernstein polinomok.
Tekintsük a meghatározása az első három fok Bezier görbe.
Lineáris görbe, a görbe az első fokú (egyenes vonal), a következő paraméter határozza meg a képlet:
Ez a kifejezés jelentése lineáris interpoláció két pont között (ábra. 1).
Ábra. 1. A görbe az első fokú (egyenes)
A másodfokú görbe, a görbe a második fokozat, képlet határozza meg:
Ez a kifejezés jelentése lineáris interpoláció a lineáris interpoláció a pontok (a 2. ábrán):
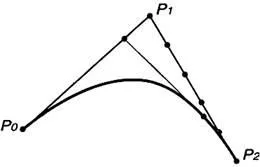
Ábra. 2. A görbe másodfokú (másodfokú görbe)
A köbös görbe, a görbe a harmadik fokozatot, képlet határozza meg:
A kifejezés egy lineáris interpoláció a lineáris interpoláció a lineáris interpoláció a pontok (3.).
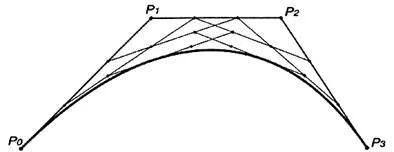
Ábra. 3. A görbe a harmadrendű (köbös görbe)