Binary keresési fák - studopediya
A bináris fa megrendelt ha bármely x csúcs igaz olyan tulajdonság: az összes tárolt elemek a bal részfa kisebb, mint az elem tároljuk x. és az összes tárolt elemek a jobb részfa nagyobb elem tárolja az x.
Fontos megrendelt fa tulajdonság: minden elemében eltérő. Ha vannak azonos elemek a fa, a fa egy részben rendezett.
A jövőben lesz-e csak a megrendelt bináris fák, a „harmonizáció” elhagyjuk.
Fa Search (keresés fák) lehetővé teszi, hogy hajtsa végre a következő műveletek Dean
dasági készletek: Search (keresés), minimális (legalább), Maximum (makro-
legfeljebb a) elődje (előző), utóda (következő), Insert (vsta-
vit) és Delete (Törlés). Így a keresési fa lehet használata
A hívás és mint egy szótár, és a sornak.
az alap működési idő arányos a fa magasságát. ha
bináris fa „sűrűn tele” (minden szinten a lehető legnagyobb
Noe csúcsok száma), magassága (és így a tevékenység végrehajtása)
arányos a logaritmusát a csúcsok száma. Épp ellenkezőleg, ha a fa predstavlya-
egyenes láncú n csúcsú, ezúttal nő fel.
Természetesen felmerülhet a gyakorlatban bináris keresési fák is
messze véletlen. Azonban különleges intézkedések elfogadásával kiegyensúlyozására de-
revev, akkor arról, hogy a magassága egy fa n csúcsú O (log n).
A műveletek végrehajtása akkor tekinthető a bináris fa képviseletében a dinamikus struktúra.
Megvalósításához az megtalálható formájában megfelelő eljárásokat.
A keresési algoritmus felírható rekurzív formában. Ha az érték kisebb, pont Fa ^ .data tovább folyik a kutatás a bal részfa ha van - keresés sikeresnek tekinthető, ha több - a keresés folytatódik a jobb részfa; keresés hibaként tekintendő, ha elérte az üres részfa, és az elem nem található.
működni TreeSearch (pont: TypeElement; Fa: PTree): logikai;
ha fa <> Ezután kezdődik a nulla
Ha a jelenlegi ^ .data = Elem majd
TreeSearch: = TreeSearch (Elem, Current ^ .Left)
TreeSearch: = TreeSearch (Elem, Current ^ .Right);
Listing 3.15 - A keresési folyamat egy bináris fa Pascal

Listing 3,24 - rekurzív keresés eljárást bináris kereső fába

Listing 3,25 - rekurzív (ismétlődő) eljárás keresésének bináris kereső fába
A minimum és maximum
Minimum gombot a keresési fa megtalálható táblákat követve balra
a gyökér (amíg el nem érjük NIL). Az eljárás visszaad egy pointert
egy minimális eleme részfájának root x.
Listing 3,26 - keresési eljárás a minimális elem bináris kereső fába
rendelési funkció biztosítja a megfelelő eljárásokat
fa-
Minimum. Ha a csúcsok x nincs bal fia, a legkisebb elem
részfa root x x. mivel bármelyik gombot a jobb részfa nem
kevesebb, kulcs [x]. Ha a bal részfa egy x csúcs nem üres, akkor a minimális
részfa gyökér elem x található a bal részfa (például
ő minden eleme a jobb részfa nagyobb).
Fa-Max szimmetrikus algoritmus:
Listing 3,27 - keresési eljárás maximális elem bináris kereső fába
Mindkét algoritmusok O (h), ahol h - a fa magassága (mert a fa csak lefelé).
A következő és az előző elemek
Hogyan talál egy bináris fa elem követi az adatokat? tulajdon
rendelési lehetővé teszi, hogy ezt azáltal, hogy a fa. Itt az az eljárás,
ami visszaad egy pointert a következő eleme x (ha az összes kulcsot
különbözőek, ez tartalmazza a következő legnagyobb gomb) vagy NIL, ha az elem -
az utolsó a fa:

Listing 3,28 - keresési eljárásokat kell (abban az értelemben, sorrendben a billentyűk) bináris kereső fa
Fa-utód eljárást külön Két esetet. Ha pra-
üvöltözõ részfa x csúcs üres, a következő eleme x minimális elem ennek a kulcsnak és egyenlő Fa-Minimális (jobb [x]).
Tegyük fel most, hogy a jobb részfa egy x csúcs üres. Akkor megyünk az x-ig
amíg meg nem találjuk a vertex, amely a bal gyermek szülei (vonalak
3-7). Ez a szülő (ha van ilyen) a kívánt elem. formálisan
szólva, a hurok a vonalak 4 - 6 megtartja a tulajdonság: y = p [Z]; keresés elem
elemek közvetlenül követi a részfáját gyökerű x.
Míg dolgozik Fa-utód eljárások magasságában h fa O (h),
mert haladunk, vagy csak fel vagy csak le.
Fa-Elődje eljárás szimmetrikus. Így beláttuk a következő tétel.
Tétel. Művelet megkeresése, Minimum, Maximum, utód és elődje h magassága a fán végrehajtásuk ideje O (h).
Hozzáadása és eltávolítása
Következő akkor tekinthető nem-rekurzív algoritmus hozzá egy elem a fa. Először is, meg kell találni a legjobb, amelyhez, mint egy gyerek, meg kell adnia egy új csúcs (valójában keresni), majd rögzítse, hogy egy új csomópontot tartalmazó tétel értékét (az eljárást írt azzal a feltételezéssel, hogy a hozzáadott elem a fa nem létezik).
eljárás TreeAdd (pont: TypeElement; var Fa: PTree);
NewNode Current: PTree;
ha fa = nil akkor kezdődik
Listing 3,31 - Eljárás egy elem eltávolítása bináris kereső fába

Listing 3,32 - Eljárás egy elem eltávolítása bináris kereső fába
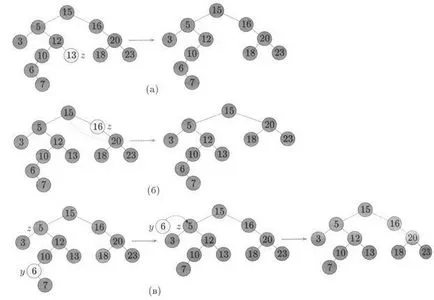
3.14 ábra - eltávolít egy elemet a bináris kereső fába
Törlése vertex z egy bináris keresési fa. (A) Ha a csomópont Z nincs gyermeke el lehet távolítani anélkül, hogy problémákat. (6) Ha a csomópont z egy gyermeke van, azt tedd a helyére vertex z. (C) Ha a vertex z két gyermek, a folyamat csökken
Az előző esetben, azaz, helyett távolítsa el a tetejétől az azonnal következő
kulcs értékét (ez a gyerek csúcsok egy), és helyezze a kulcsot KEU [y] (és a kapcsolódó
további adatok), hogy helyezze a vertex z.
A fa kezelési folyamat alkalmaz fordított bejárás módszert. Reverz megoldás biztosítja, hogy először látogatható, és eltávolította az összes leszármazottai az ős eltávolítása előtt maga őse.
eljárás TreeClear (var Fa: PTree);
ha fa <> Ezután kezdődik a nulla
Listing 3,33 - Eljárás bináris keresési fa elszámolási
Időbonyolultsága E művelet O (n).
Véletlen keresési fák
Véletlen keresési fák rendezett bináris keresés fák, létrehozását, amely az elemek (kulcsok) egészül ki, véletlenszerű sorrendben.
A létesítmény egy ilyen fák segítségével ugyanazt az algoritmust, ha hozzá csúcsok bináris kereső fába. Létrehoz egy fa véletlenszerűen, vagy nem, ez attól függ, hogy milyen sorrendben az elemek jönnek hozzá. Példák a különböző fák alapján létrehozott különböző FIFO elemek az alábbiakban adjuk.
Ábra 3.15 - Random és degenerált keresési fák
Az elemek érkezésekor véletlenszerűen kap egy fa minimális magasságú h (lásd. Ábra. 3.12.a), és ennek megfelelően csökkenti a keresési idő elem olyan fa, amely arányos O (log n). Az elemek érkezésekor rendezett módon (lásd. Ábra. 3.12.b), vagy egy kissé szokatlan módon (lásd. Ábra. 3.12.v) az építmények degenerált keresési fák (ez fajul lineáris listát), hogy nem csökkenti a keresési időt, amely O (n).
Optimális keresési fák
Ha keres egy bináris fa egyes elemek kereshetők gyakrabban, mint a többiek, vagyis van egy valószínűségi pk Keresés k-adik eleme és a különböző elemeket, ezeket a valószínűségeket nem ugyanaz. Tudod csak feltételezik, hogy a keresést a fa közepén gyorsabb lesz, ha ezeket az elemeket, amelyek a keresett gyakrabban lesz közelebb a gyökér a fa.
pi - annak a valószínűsége, hogy a keresési érv Ki;
q0 - annak valószínűsége, hogy a keresési álláspontja kevésbé, mint a K1;
qn - annak valószínűsége, hogy a keresési érv nagyobb Kn;
Ezután a keresési fa árát C fogja meghatározni az alábbiak szerint:
ahol levelrootj - szintű csomópont j. és levellistk - lapos szinten k.
keresési fa nevezzük optimális, ha az ár minimális, vagy más szóval, az optimális bináris keresési fa - ez egy bináris keresési fa alapján szerkesztettük teljesítmény maximalizálásához egy adott eloszlása szükséges adatok keresési valószínűségek.
Van olyan megközelítés építésének optimális keresési fák mely elemek kerülnek beillesztésre csökkenő frekvencia, amely átlagosan jó kereső fák. Azonban ez a megközelítés, hogy egy degenerált keresési fát, ami messze van az optimálistól.
Egy másik megközelítés, hogy kiválassza a gyökere k, hogy a maximális összege valószínűségek a csúcsai a bal részfa és a jobb részfa olyan kicsi volt, amennyire csak lehetséges. Ez a megközelítés is lehet rossz a választása esetén, mint a gyökér elem értéke kicsi pk.
Vannak algoritmusok, amelyek lehetővé teszik, hogy építsen egy optimális keresési fa. Ezek közé tartozik például az algoritmus Garcia Vocea. Azonban, ezek az algoritmusok egy ideje komplexitása érdekében O (N 2), és néhány még azonos térbeli komplexitás. Így létrehozása optimális keresési fák igényel sok rezsiköltségek, amelyek nem mindig igazolják a nyereség gyors keresést.