Bizonyítsuk be a Pitagorasz trigonometrikus azonosság

Pitagorasz-trigonometrikus azonosság a következő egyenletet:

sin2 α + cos2 α = 1

Ez azt jelenti, hogy egy derékszögű háromszög a négyzetének összege a szinusz és koszinusz azonos hegyesszög egyenlő eggyel.

Lássuk be ez trigonometrikus azonosság. Adott egy ABC derékszögű háromszög (∠C = 90o). Felhívjuk a magassága az átfogó CH.

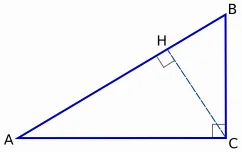
Fejezzük a lábát az ABC háromszög a koszinuszok. Mivel cos A = AC / AB, majd

Mivel cos B = BC / AB, a

Most tekintsük a háromszög ACH. Igaza van, t. Hogy. CH ⊥ AB. Mivel ebben a háromszög átfogója. Ezután cos A = AH / AC. Mi kifejezni itt a szegmens AH:

Mi helyettesíti AC szakasz annak kifejezett érték korábban a koszinusza szög ABC háromszög. kapjuk:

AH = (AB · cos A) · cos A = AB · cos 2 A

Most tekintsük a háromszög BCH. Ez cos B = BH / BC. Fejezzük BH BC és kicserélni a talált érték az ABC háromszögben:

BH = AB · cos 2 B

A hossza AB a hosszának összegét AH és BH:

Cserélje ki az AH és BH azok kifejezések szempontjából koszinuszok:

AB · cos 2 A + AB · cos 2 B = AB
AB · (cos 2 A + cos 2 B) = AB
cos 2 A + cos 2 B = 1

Mint ismeretes, a derékszögű háromszög egyenlő az koszinusza hegyesszög egy másik azonos háromszög szinusz a hegyesszög. Ebben az esetben:

Következésképpen, a személyazonosító cos A + cos 2 2 B = 1, akkor cserélje ki a koszinusza a B szög a sine a szög A. Így kapjuk:

cos 2 A + cos 2 B = 1
cos 2 A + (cos B · cos B) = 1
cos 2 A + (sin A · sin A) = 1
2 cos 2 A + sin A = 1

Így, az összeg a tér a koszinusz a szög és a tér a szinusz a szög egyenlő az egység, szükség szerint.