Cat Arnold - Saratov csoport elméleti nemlineáris dinamika
Bemutatás a „macska Arnold”
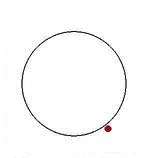
Köztudott, a szakirodalomban tükrözi „Arnold a macska.” (Az elsődleges jelek értékei dinamikus változók kapcsolatos következő diszkrét idejű lépés.) A fázis helyet a rendszer általában úgy értelmezik, a felület egy tórusz, amelyben egy változó be van állítva a koordináta a párhuzamos, a másik mentén meridián a tórusz, mind meghatározott időintervallumra 0-1. kényelmesebb használatát grafikonok az egység téren, tekintettel arra, hogy az egymással szemben lévő oldalát is azonosítottak. A név eredete van annak a ténynek köszönhető, hogy Mr. Arnold, aki azt javasolta, ezen a térképen egy példa a rendszer kaotikus dinamika tóruszon illusztrálta akció segítségével a kép formájában a macska feje (lásd. ábra.).
A következő Arnold macska osztályába tartozik a konzervatív rendszer: a hatása alatt olyan megjelenítési területen (például a macska feje) őrzi a területet. Ismeretes, hogy ez a térkép mutatja a kaotikus dinamika abban az értelemben, az axiomatikus elmélet hiperbolikus Anosov. Két Ljapunov exponens megjelenítéséhez Arnold macska
Megjegyezzük, hogy a vezető alakja pozitív. Néhány további információt kijelző Cat Arnold és egyéb térképeket a tórusz megtalálható a szakasza, a honlapon szentelt kvantum káosz.
Ahhoz, hogy további hasznos megjegyezni, hogy a leképezés Arnold macska is képviselteti magát a kétszeres alkalmazása egyszerűbb térképezés
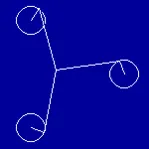
Ami a fizikai megvalósítása Arnold macska kijelző, úgy a négy oszcillátor kapcsolt nem autonóm van der Pol
Itt x. y. Z és W generalizált koordinátákat oszcillátorok, A - amplitúdó moduláció vezérlő paraméter, T - modulációs időszakban, amely, ahogy azt kell feltételezni, tartalmaz egész számú időszakok sajátrezgéseinek 2 # 112; / # 119; 0. # 101; - kapcsolási paraméter.
A rendszer a következőképpen működik. Legyen az első és a második oszcillátor generáló lépést oszcillál fázisok rendre Fx és ~ y.
míg a második pár oszcillátor alatt van lasing küszöböt. Az átmenet egy szakaszában gerjesztés a második pár, a harmadik rendszer oszcillátor z van kitéve vetőmag megfelelő jelet a terméket xy és tartalmaz egy rezonáns oszcillátor ezt az összetevőt kétszeres frekvencia:
Így a rezgések a harmadik oszcillátor fázisban kapott Fz = Fx + ~ y. Negyedik oszcillátor w izgatott csak a frekvenciája, az x # 119; 0 úgyhogy Fw = Fx. Továbbá, amikor generáló lépést a második pár oszcillátorok végén, w a vetőmag jel az oszcillátor y. bejövő gerjesztési lépést, és Z jel összekeverésével egy referencia frekvenciájú jelet # 119; 0. előírja vetőmag oszcillátor x. által adott a második kifejezés a képletű
Ennek eredményeként, egy új gerjesztési lépés az első és a második oszcillátor fázisban kapott rendre F'x = Fz = Fx + és F'y ~ y = Fw = Fx. Figyelembe véve, hogy a fázisokat meghatározott legfeljebb egy adalékanyag 2 # 112; és bevezetése standardizált változók q = Fx / 2 # 112; és p = ~ y / 2 # 112;. Eljutunk a leképezés p „= q. q „= p + q (mod 1), kétszeres amelynek használata, mint már említettük, egyenértékű Arnold macska leképezés. Az alábbi ábra mutatja a kapcsolatot a változók az idő x. y. Z és W jelentése a már átesett egy kaotikus mozgások összhangban a leírt mechanizmus. A fényképek eredményei alapján a numerikus megoldása egyenletek # 119; 0 = 2 # 112;. T = 20, A = 2, # 101; = 0,4.
Káosz megnyilvánul a véletlen bolyongás a magasságra és a mélypontra a boríték képest a tölteléket. Való megfelelés bizonyítására a fázis dinamikáját Arnold macska térkép, végrehajtja a következő eljárást. Végezzük numerikus megoldása egyenletek, és egy bizonyos ponton megfelelő a középső szakasz a gerjesztés az első és a második oszcillátor meghatározzák fázisok a kapcsolatok
Ha a pont koordinátái (Fx. ~ Y) beleesik a „macska fejét”, hogy ábrázolja őt a rajz, és a következő két grafikon pont (Fx ~ y) az időben 2T és 4T. Miután felhalmozódó egy kellően nagy számú pontot szövőszék „macska fejét”, és a képek után egy és két iteráció Arnold kijelzőn. A kapott képeket össze lehet hasonlítani a közvetlenül a Arnold ismétléseket a térkép. Megfelelés érhető el, ha be mindkét egyenlet adalék állandók, amelyek megfelelnek bizonyos állandó mellett a fázisban keletkező átadás zavarok oszcillátor közötti. Tekintettel ezekre, választott empirikusan egy adott állandó üzemmódban, a kijelző van módosítva ezáltal:
Hasonlítsuk össze a két alábbi sorozata grafikonok betartásának biztosítása érdekében kiemelkedő dinamikát fázisában a javasolt rendszer és a dinamika a módosított Arnold macska térképet.
Az utolsó ábra egy telek két idősebb Ljapunov kitevőket a kapcsolt rendszer oszcillátorok nem autonóm Van der Pol a lassú modulációs amplitúdó rögzített egyéb paraméterek, és a kapott egységnyi idő alatt 2T.
Amint látható, számos paraméter mindkét Ljapunov exponens közelítőleg állandó marad jó értékekkel összhangban várható megjelenítésére Arnold macska.
Megjegyzés. Ha a megközelítés, hogy a rendszer dinamikáját formálisan, tekintve az épület a stroboszkóp-Poincaré térkép, csökkenti az ismétléseket egy 8 dimenziós megjelenítés. Valóban, a pillanatnyi állapota a rendszer határozza meg egy sor nyolc változó V = x. dx / dt. y. dy / dt. z. dz / dt. w. dw / dt>. Ha egy bizonyos t = nT beállított állapot vektor Vn. A megoldások az egyenletek kimondják révén nyert 2T időszakban. Vn + 1 = F (Vn). A 8-dimenziós térben hangszóró közelében fordul elő a két-dimenziós tórusz, amely meghatározhatja a koordinátákat kétfázisú engedelmeskedik Arnold macska feltérképezése. A többi a koordináták egy erős tömörítés.
Szaratov csoport
elméleti nemlineáris
hangszórók