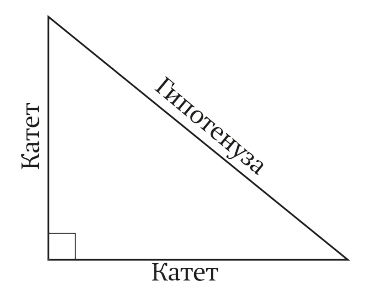
derékszögű háromszög
By the way, ha jól emlékszem, amit a lábak és az átfogó? Ha nem, akkor nézd meg a képet - frissítő a tudás
Lehetőség van arra, hogy több alkalommal is használta a Pitagorasz-tétel, de ha azon, hogy miért egy ilyen tétel igaz. Milyen lenne bizonyítani? És legyen eljárni, mint az ókori görögök. Rajzolj egy négyzet oldala $ latex a + b $.
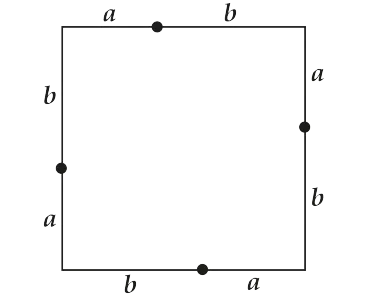
Lásd milyen ügyesen van osztva az ő oldalán a hossza a szegmens $ latex egy $ és $ b $ latex!
És most csatlakozik a megjelölt pontok
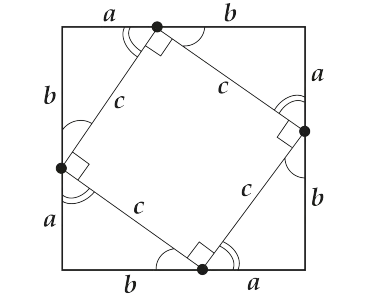
Mi az a terület, a nagyobb tér? Ez így van, $ latex ^> $. Egy kisebb területen? Természetesen $ latex c ^ 2 $. Ott volt a teljes terület a négy sarkából. Képzeljük el, hogy mi tartott két és nekidőlt egymást átfogója. Mi történt? Két téglalapok. Tehát, a terület a "hulladék" a $ latex \ displaystyle 2ab $.
Most nézzük összegyűjti az összes együtt.
Tehát megnéztük Püthagorasz - bizonyult a tétel ősi módon.
Derékszögű háromszög trigonometria és
Az alábbi relációk a derékszögű háromszög:

I. $ latex \ displaystyle \ sin \ szög = \ frac; \ \ \ sin \ szög B = \ frac \ $
Sine a hegyesszög egyenlő az arány a másik lábát, hogy az átfogó
II. $ Latex \ displaystyle \ cos \ szög = \ frac; \ \ \ cos \ B szög = \ frac $
A koszinusza hegyesszög egyenlő az arány a átfogója a szomszédos láb.
III. $ Latex \ displaystyle tg
\ A szög = \ frac; \ \ tg
A tangense hegyesszög egyenlő az arány a másik lábát, hogy egy szomszédos láb.
IV. $ Latex \ displaystyle ctg
\ A szög = \ frac; \ \ CTG
Kotangensét hegyesszög egyenlő az arány a szomszédos láb ellentétes befogó.
És még egyszer az egészet tabletták:

$ Latex \ displaystyle \ sin \ szög = \ frac $
$ Latex \ displaystyle \ sin \ szög B = \ frac $
Derékszögű háromszög egybevágó, ha a láb és a hegyesszög egy háromszög egyenlő a lábát, és hegyesszög másik háromszög.
Figyelem! Nagyon fontos, hogy a lába „megfelelő”. Például, ha van ilyen:
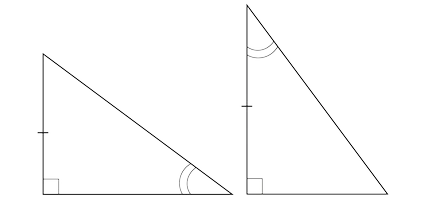
Ez háromszög nem egyenlő. annak ellenére, hogy ennek következtében rendelkeznek egy azonos hegyesszög.
Szükséges, hogy mind a háromszögek lába egy szomszédos, vagy mindkettő - ellentétes.
Észrevetted a megjelölések közti különbségek az egyenlőség derékszögű háromszögek a szokásos jelei egyenlőség háromszögek? Nézz be a témát a „háromszög”, és felhívta a figyelmet arra, hogy az egyenlő a „rendes” háromszög szüksége egyenlőség a három elem: a két fél, és a köztük lévő szög, a két szög és az oldalsó két vagy három oldalról. De az egyenlő derékszögű háromszögek elég csak két megfelelő elemeket. Ez jó hír, nem?
Hasonló a helyzet, és a hasonlóság a funkciók négyszögletes háromszögek.
Tünetei derékszögű háromszögek hasonlósága
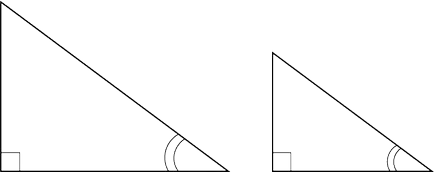
Ha a derékszögű háromszögek ugyanazon a hegyesszög. ezek hasonlóak.