Diffrakciós elektromágneses hullámok tartalom platform
33. diffrakciós az elektromágneses hullámok.
Geometriai optika csak akkor igaz, ha a hullámhossz lehet tekinteni, mint egy végtelenül. Ha ez nem így van, akkor a megfigyelt eltérések geometriai optika, a jelenség a diffrakciós törvényeket. Kiszámításához a diffrakciós mintázat volt által javasolt Huygens-Fresnel elv, amely szerint minden egyes pontja a hullámfront egyik forrása a másodlagos hullámok és a diffraktált hullám kapjuk eredményeként a beavatkozás.
A matematikai megfogalmazása a Huygens-Fresnel elv adta Kirchhoff. Figyelembe vesszük a skalár diffrakciós monokromatikus hullámok. Abban az esetben, az elektromágneses hullám ilyen skalár mennyiség lehet, például - az elektromos mező vektort komponense a hullám. Ez skalár elmélet közelítő, de mégis, ez elég kielégítő leírja a diffrakciós fény egy kis eltérés a jogszabályok geometriai optika, ami nagyon fontos a műszeres optika.
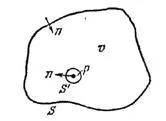
(2). amelynél ez az érték a normál, hogy a belső felület. Ha a funkció is kielégíti az (1) egyenlet, a bal oldali részét (2) nulla. A funkciók veszi egy gömb alakú hullám -, ahol - a mért távolság az a pont. Ez a funkció a szingularitás a ponton, így körülveszi őt szféra és a Green-formula alkalmazható hangerő és között. . mező integráció az (amikor a gömb sugarának nullára). Aztán végül kapjuk: (3) Ez a képlet a Helmholtz-Kirchhoff. Így annak érdekében, hogy a területen egy bizonyos ponton a kötetben, tudnunk kell, hogy az elosztó a területen, és a szokásos származék felületén a kötet.
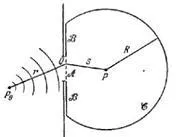
Tekintsünk egy diffrakciós monokromatikus hullám egy pontban a nyílás a képernyőn. Ahhoz, hogy megtalálja a pályáról a ponton meg kell számítani a (3) integrál a teljes zárt .no felületi integrál szféra tekinthető nullával egyenlő. Ez így van, ha feltesszük, hogy a sugárzás nem létezett a végtelenségig, és nem volt ideje, hogy elérje a határokat a szférában. Azaz, mi egy kicsit távolodjon el a feltételeket, a monokróm (monokromatikus sugárzást mindig ott van), de fizikailag minden rendben. Aztán ott van az integrál a terület fölött a lyuk. Vegye figyelembe, hogy, akkor a (3) kapjuk (4). Most, ha a felület válasszon egy gömb alakú hullám első forrást, ezt kapjuk:
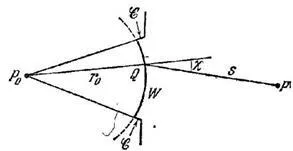
Látható, hogy a (4) van szimmetrikus a forrás és egy pontot. Ez a forrása az azonos intenzitású elhelyezett pont járna az azonos hatású teszi a pontot. Ez a Helmholtz viszonosság tétel.
A fentiekből következik azonnal következtetni a fényeloszlást diffraktált további képernyők egymáshoz, azaz. E. A képernyőkön, amelyben egy furat esnek pontosan egybe más átlátszatlan részek, és fordítva. Let - Integrált zavar, ha csak az egyik képernyő útjába helyezett között a forrás és a megfigyelő pontot. Aztán, ahogy úgy reprezentálható, mint integrálok át a lyukak, és a lyukak a további képernyő úgy vannak elrendezve, hogy a teljes mértékben „nyitott” a teljes hullámfront, a
Ez az úgynevezett elve Babinet.
A következő következtetéseket lehet levezetni Babinet elve. Ha, akkor, r. E. A pontokat, ahol az intenzitás jelenlétében egy képernyőn egyenlő nullával, jelenlétében csak egy másik képernyőn ez lesz ugyanaz, mint annak hiányában a képernyők. Olyan helyeken, ahol hiányzik képernyők, és egyenlő amplitúdójú és különböznek fázisban.
Fraunhofer és Fresnel diffrakció.
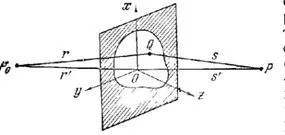
Tekintsük a integrál (4). Amikor integrálja a lyukba, hogy megváltoztatja sokkal gyorsabb, mint, és emellett, ha a két pont közötti távolság, és a képernyő nagy, akkor. Amennyiben - a szög a normális, hogy a képernyőn, és egyenes. Ezután (4) lehet újraírni az alábbiak: (5) (és a távolságok a pontot). Derékszögű koordináta-rendszer elején. Ebben a koordinátarendszerben :. Most szeretnénk menni a koordinátákat, és (nézd meg a koordináta tengelyeket a képre!), Ez a változás a nyílás síkjában. Ha ez megtörténik, akkor kap:
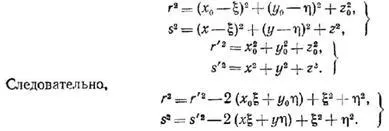
Ezután találunk és bővülő hatáskör ,,,.
Behelyettesítve ezeket az értékeket (5), megkapjuk:
Ha most sem hagyhatja figyelmen kívül szempontjából nagyságrenddel nagyobb, mint 1, és akkor foglalkozik a Fraunhofer diffrakciós. Ha a másodfokú és magasabb szempontból nem elhanyagolható, hogy Fresnel diffrakció. Nyilvánvaló, hogy a Fraunhofer közelítés alkalmazható, ha a forrás és a megfigyelési pont közelében található a tengely és a távolság a képernyőn. Ez megfelel a helyzetet, amikor az eltérés geometriai optika nem túl nagy.
Általában figyelmen Fraunhofer diffrakciós eljárással gyűjtőlencse, és az egész diffrakciós mintázatot kapunk a fókuszsíkra. Ez azért lehetséges, mivel a lencse nem vezet be további útvonal közötti különbség sugarai megy az egyik pont a képet.
Fraunhofer diffrakciós egy téglalapot.
Nézzük a diffrakciós fény egy téglalapot. A (6) van véve csak az első két kifejezést.
És a fény intenzitását, ahol - az intenzitás a kép közepén.
Abban az esetben, diffrakciós fény hosszabb összefüggéstelen forrásból kell összefoglalni intenzitása minden pontján a forrás. Ha más forrásból pontok következetes, meg kell integrálni kompleksnyeamplitudy.
Például, abban az esetben a diffrakciós fény egy vékony huzal hosszú rés, az intenzitás eloszlás adott. .
Vegye figyelembe, hogy olyan (7) egy kétdimenziós Fourier-transzformáció egy mező a képernyő felületét. Amikor a hullámfront korlátozott, Fourier jelennek síkhullámok szaporító különböző szögek - vagyis a diffraktált hullám.
37.Effekt Zeeman és Stark-effektus.
Tekintsük a Hamilton-egy atom elhelyezett egyenletes mágneses mezőt.
Ahol az összegzés van az egész elektronok, a kölcsönhatás energiája elektronok a sejtmagokat és a egymással, a teljes elektron spin üzemeltető atom, egy vektor potenciál mező. Ebben az esetben ez egy homogén mágneses mező: (2).
Tekintsük a kapcsoló, amikor a potenciális a vektor kiválasztott formájában (2), és így, a generalizált impulzus operátor commutes az üzemeltető. Ezekkel zárójelben a nyilvánosságra hozatal (1). kapjuk:
Behelyettesítve a 2 kapjunk.
-üzemeltetője a teljes orbitális perdület az atom.
Attól függően, hogy az intenzitás a mágneses mező tudja különböztetni 3 esetben felosztása a energiaszintek az atom:
Egy gyenge mágneses mező, figyelmen kívül hagyjuk a kifejezést másodfokú terén; szintű felosztása miatt a mágneses mező kisebb a távolság, a szintek közötti finom struktury- rendellenes Zeeman-effektus. Gyenge területen. Még figyelmen kívül hagyjuk a másodfokú kifejezéseket, de a szint hasító értéket meghaladja, a finom szerkezetű. Paschen-vissza hatás. Nagy területeken a másodfokú kifejezés figyelembe vételével, - a másodfokú Zeeman-effektus.
Rendellenes Zeeman-effektus.
Ebben az esetben az üzemeltető a zavar. A háborítatlan energiaszint független a vetülete a teljes lendület, ezért szükséges alkalmazni perturbációszámítás a degenerált szinten. Tekintsük a mátrix a perturbáció üzemeltető: ha az üzemeltető a teljes perdület az atom, és a háborítatlan hullám funkciókat.
Nyilvánvaló, hogy (3). Továbbá, meg kell kiszámítani (4). Azt feltételezzük, hogy ez a szint tartja LS kapcsolat, vagyis ez jellemzi bizonyos értékeit L, S, J.
Kiszámításához (3), és a összefüggéssé nyilvánvaló. Mivel az L, S, J határozzuk értéket a feltétellel, hogy az érték lehet helyettesíteni a sajátértékek. Aztán kapunk: És végül: Ez a perturbáció mátrix diagonális, így megzavart energia szintet, ahol a Lande tényező ezen a szinten. Látjuk, hogy szeres degenerált szint szünetben degenerációja teljesen visszavonult. Megjegyezzük, hogy a hasítási lehet jelen és ha például olyan állapotban.
(Megjegyzés: A másik következtetés megtalálható Landau, és még jobb, hogy hogyan jelenítse meg Golubovskii - hol vektorok előrehalad és minden)
Abban az esetben, ha a mágneses mező nagyon nagy, és meghaladja a Zeeman felosztása a finom szerkezetű intervallumok előző részben képleteket helytelenek. Ebben az esetben az energia a mágneses tér sokkal nagyobb, mint a spin-orbitális interakció. Ezért, mint a első közelítésben elhanyagoljuk közötti kölcsönhatás ezen.
Ezután megszakad a kapcsolat vektorok közötti L és S, és elkezdenek függetlenül kvantáljuk az irányt a mágneses mező, vagyis akkor van értelme, nem csak a nagyságát, hanem és. Aztán :.
Tekintsünk egy atom állandó elektromos mező. Mivel a területen van egy tengelyirányú szimmetria, a tárolt vetülete a teljes lendületet a villamos tér irányában. Ugyanakkor jelentős különbség összehasonlítva a mágneses mező abban a tényben rejlik, hogy további energiát függ csak az abszolút értékeket. Ezért a degenerált állapota ugyanaz. Az eredmény egy nem teljes felosztása a szinten ezt figyelembe sublevels értékekkel: -with egésze, azaz az al-réteget. És fél egységet sublevels a -on értékeket.
Azt a kérdést, a függőség a Stark felosztása az elektromos mező. További energia rendszer, amelynek dipolusmomentum az elektromos mező. Ha tehát van egy lineáris jelenség Stark.
Azonban, ellentétben a mágneses momentum, dipólmomentum nem kvantált, és az előre meghatározott rendszer állapotát jellemzi átlagértéket ezt a pillanatot. A rendszerek központi szimmetria (atomok, molekulák Homonukleáris) az átlagos értéke a dipólmomentum nulla. Ezért az ilyen rendszerek lineáris Stark hatása a mező nem figyelhető meg.
Ugyanakkor a rendszer kerül elektromos mező szerezhetnek az indukált dipólus momentum, amely, ha nem túl erős mezőket arányos: ahol -polyarizuemost (megjegyzendő, hogy a molekulák, hogy - tenzor). Ezután a további energia egyenlő lesz.
Az erős területeken, ha további energia összemérhető a távolságot a szintek is megfigyelhető jelenség lineáris Stark. Az ilyen hasítási megfigyelhető a hidrogénatom.
A polarizálja az atom függ. Körülbelül ez az összefüggés az alábbiak szerint :. Így.
Festés Stark felosztása egy spektrális vonal határozza meg a felosztása kombinálásával szintek és kiválasztási szabályok. Érdemes megjegyezni, hogy az érték a másodfokú Stark felosztása mindig kicsi, és összege töredéke.
Ennek eredményeként, a Stark kiszélesedik ütközések töltött részecskék (például csillag vagy plazma) fordul elő folytonosság szintű elmozdulás kisebb energiák felé. Continuum kezdődik szint száma, amikor a Stark szélesítése nagyságrenddel nagyobb, mint a távolság a szintek között.