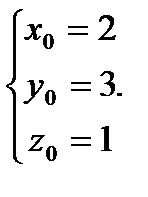egyenes egyenlete az űrben - studopediya
A térben közvetlenül a. A ponton áthaladva párhuzamosan a vektor. úgynevezett útmutató és közvetlen vektort (14. ábra).
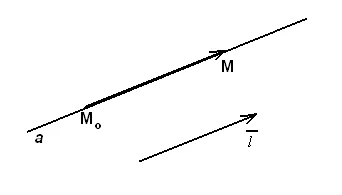
Hagyja, hogy a pont - a pont egyenáram. Vector fekszik az egyenes és egy egyenesen. A feltétele kollinearitása két vektor, van:
Ezek az egyenletek - a kanonikus egyenletek egy egyenes vonal a térben.
Ha a kanonikus egyenletek bevezetésére t paraméter:. Megkapjuk a paraméteres egyenleteket a sor:
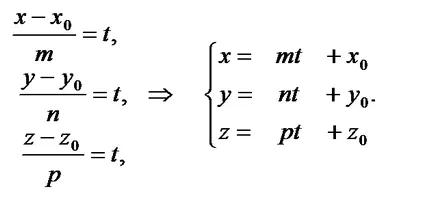
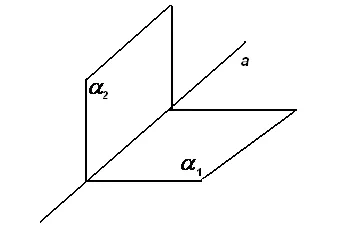
Vonal lehet meghatározni, mint a két síkja egymást metszi (15. ábra):
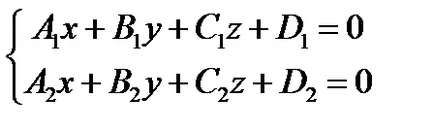
egyenes egyenlete áthaladó két pont.
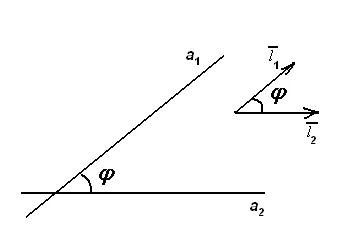
A szög a sorok között egyenlő a hegyesszög közötti irányvektor (ábra16) és kiszámítása a következő képlettel:
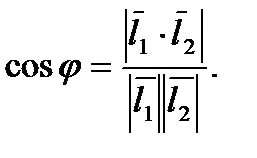
Példa. Közvetlen set egyenletekkel
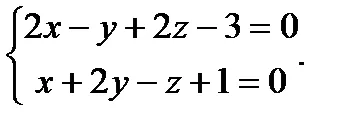
a) Írja a sorban a kanonikus és paraméteres egyenletek;
b) Mekkora a szög az egyenes és az egyenes által megadott egyenletek
a) Válassza ki az egyik pont, amelyen keresztül adja át az említett vonal metszése által meghatározott síkok. A kezdeti rendszernek van egy végtelen számú megoldást, melyek közül az egyik megkapta az egyik változó, amely egy bizonyos értéket. Let. akkor az értékek a többi ismeretleneket talált a rendszer
A megoldás ez a rendszer egy számpár.
Ennek eredményeképpen megkapjuk a lényeg. amelyen keresztül a kívánt sort. Mint egy útmutató is részt vehet a közvetlen vektor-vektor. hol. - a szokásos vektorok síkok a határvonalat átlépő, amely egy egyenes vonal. Így
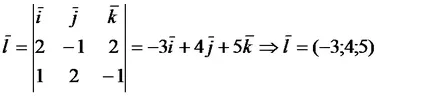
Írjuk fel a kanonikus egyenletek egy egyenes vonal.
Kapjuk a kanonikus paraméteres egyenleteket az egyenes:
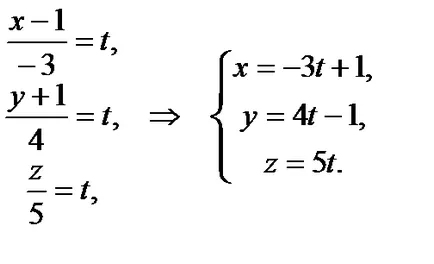
b) az irányvektor a sor. irányvektorát egyenes közötti szög a vonalak, és egyenlő a hegyesszög közötti irányvektor:
A szög az egyenes és a sík
Tegyük fel, hogy adott egy egyenes és sík (17. ábra):
Közvetlen c irányvektor
A sík normál vektor
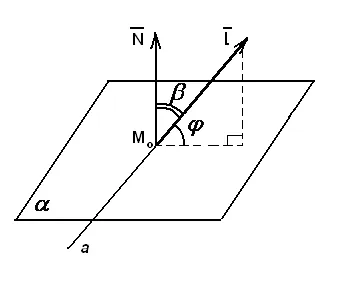
A szög közötti egyenes vonal és a sík képlettel számítottuk ki:
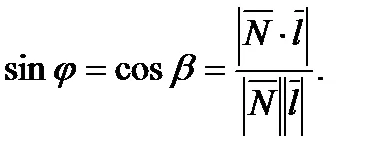
Ahhoz, hogy megtalálja a metszéspontján vonal és sík. Meg kell irányítani paraméteres egyenletek
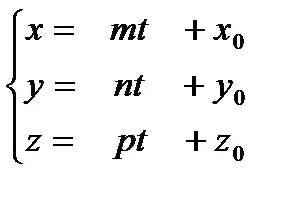
Példa. Keressen egy) közötti szög egyenes és a sík;
b) a metszéspontját vonal és sík.
.
Határozat. - síkjára merőleges; - az irányvektor a sor.
b) helyettesíteni a paraméteres egyenleteket az egyenes
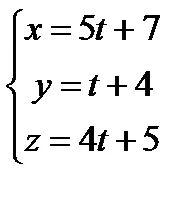
. - beállítása metszéspontján vonal és sík.
Mi helyettesíti a paraméter értékét a paraméteres egyenleteket, megkapjuk: