Elemei vektor algebra
1.1. Vektorok euklideszi térben
Ezzel szemben a skaláris mennyiségek, amelyek teljes mértékben jellemzi a számszerű értéket a választott rendszernek egységek (hőmérséklet, munka, sűrűség, stb), vektor nagysága, mint a számszerű érték, szintén az irányt a térben (például teljesítmény és sebesség).
Az iskolai matematika ismert, hogy a vektor is képviselteti magát egy irányított szakaszt, azaz egy vonal szegmenst, amelyek bármely adott pontban a kezdet és a végén, amely, és ahol az említett skála egység (ábra. 1.1).
Ha pont a kezdet, vég aB vektor, vektor felírható
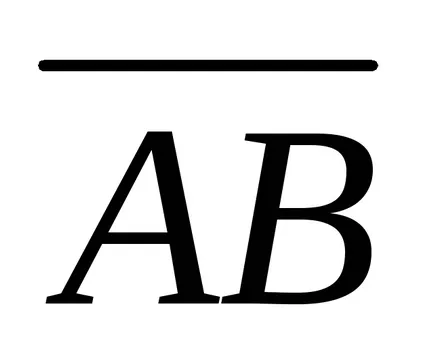

A számértéke vektor olyan vektor egységet. Előfordul, hogy a készülék vektor hossza. Modul, vagy a vektor hosszának jelölik |
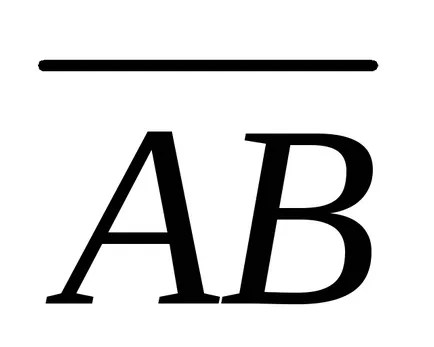

Vektor, amelynek eredete egybeesik a végén, az úgynevezett nulla. Vektorok találhatók, egy egyenes vonal vagy párhuzamos vonalak, és a kijelölt nazyvayutsyakollinearnymi
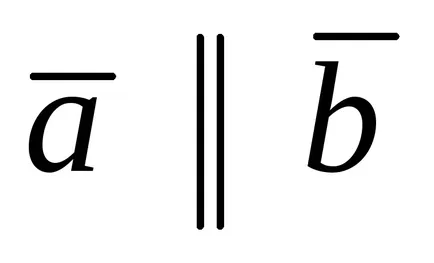
Két vektor akkor mondjuk, hogy megegyezik, ha azonos nagyságú és irányú
Vektor összeadás és szorzás számmal.
Minden osztály a vektorok (például, mozgás, sebesség, erő, mágneses mező intenzitás) lehet meghatározni műveletet ismert vektor összeadás és szorzás számmal.
A hozzáadást történhet segítségével a paralelogramma. vagy - kötél sokszög.
terméket a vektor


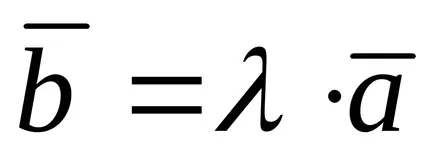
3). vektorok

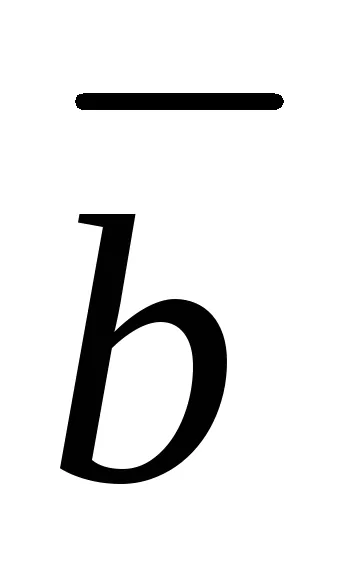


Vektorok alkotnak lineáris tér