Ellipszis és kanonikus egyenlete

Definíció 3.5.2. Ellipszis a készlet minden pont a síkon, az összeget
A távolságok, amelyek a két adatpont ezen a síkon, az úgynevezett gócok vannak
állandó érték egyenlő 2a.
A kanonikus egyenlete ellipszis adják

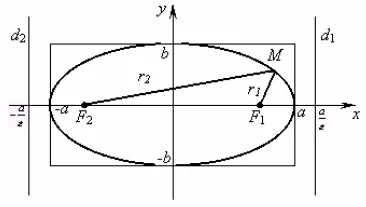
ahol egy - félig nagytengelye van; b - kisebb tengely. Pontok F1 (c, 0) és F2 (-c, 0) - c úgynevezett
gócok az ellipszis, az ellipszis alakú (egy intézkedés a tömörítés) jellemzi a
különcség
Definíció 3.5.3. Focal sugara a távolság a görbe egy fókuszpontot.
Focal ellipszis sugarak r1 és r2 rokonságban
Az ellipszis társított két nagy vonalak nevezzük directrices d1 és
d2. akinek egyenleteket a formában. Az arány a távolságok bármely pontjáról az ellipszis
koncentrálni a megfelelő távolság az első tengely az ellipszis egyenlő direktrixét # 949;.

Egy különleges eset az ellipszis egyenlet, ha az egyenlet egy kör középpontú O pont (0,0) és a sugár egy. A kanonikus egyenlete egy kört
központ azon a ponton, O „(a, b), és r sugarú adják.
Egyéb kanonikus egyenlete elliptikus görbék:
1. egyenlet megadja az O pont (0,0);
2. egyenlet meghatározza egy képzeletbeli ellipszis;
3. Az egyenlet határozza meg a képzeletbeli kör.