Előadás 2 elfogulatlan és konzisztens becsléseket a tényleges eloszlás paraméterei
Annak érdekében, hogy a statisztikai becslés jó közelítéssel a becsült paraméterek, akkor kell elfogulatlan és hatékony gazdag.
Elfogulatlan úgynevezett statisztikai értékelés


Megmozdult az úgynevezett statisztikai értékelés


Hatékonyan úgynevezett statisztikai értékelés


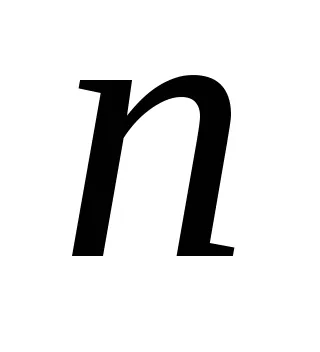
Gazdag az úgynevezett statisztikai értékelés


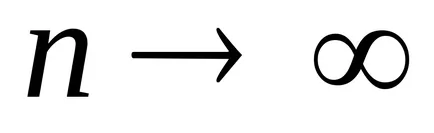
A minták különböző méretű kapunk a különböző értékeket a számtani átlag és a statisztikai diszperziót. Ezért a statisztikai átlag és szórás véletlenszerű értékeket, amelyre nincs várakozás és a szórás.
Mi kiszámítani a várható értéke és szórása a számtani átlaga. Jelöljük

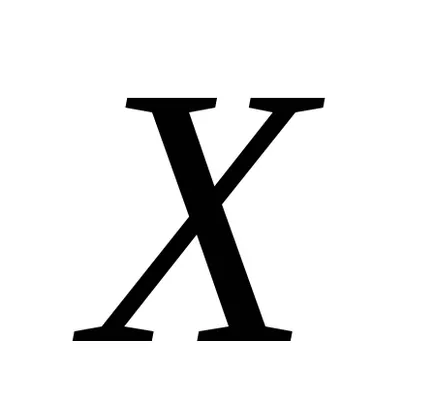
Itt is, mint a véletlen változók figyelembe venni:
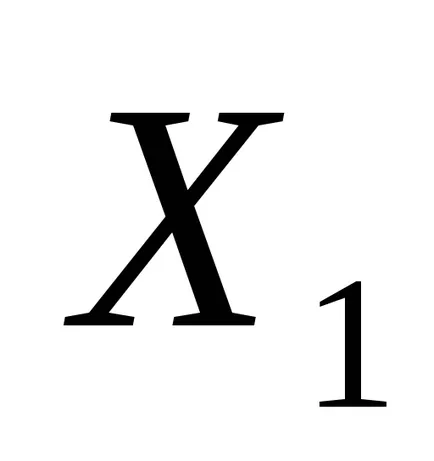

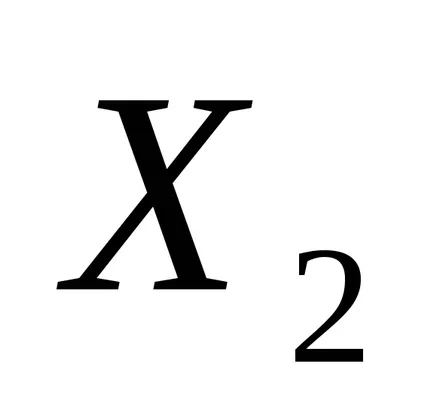
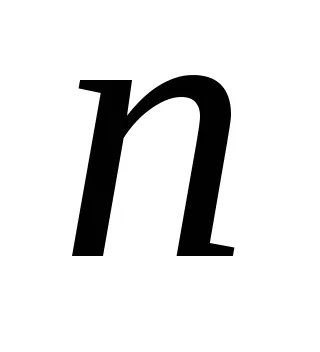


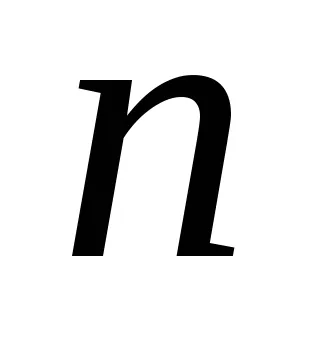
.
Től képletű (1), hogy a számtani átlag torzítatlan becslését az elvárás, mert a matematikai elvárás egyenlő a számtani átlagát matematikai elvárás egy véletlenszerű változó. Ez a becslés is összhangban áll. A hatékony ez becslés típusától függ véletlen változó eloszlása
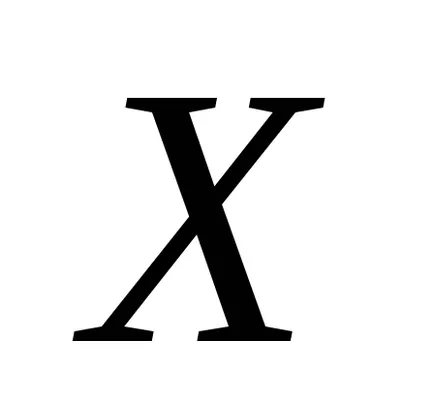
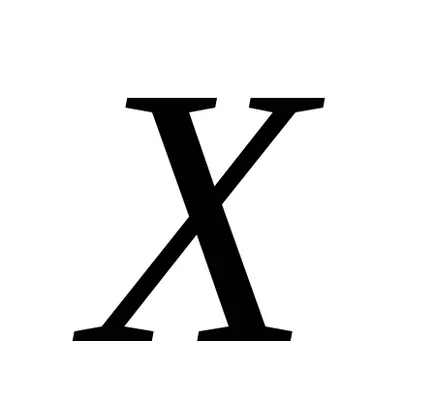
Most azt látjuk, a statisztikai értékelés diszperziós.
A kifejezés a statisztikai diszperzió lehet konvertálni az alábbiak szerint:
Most azt látjuk, a várható statisztikai szórás
Formulából (6) azt mutatja, hogy a várható statisztikai diszperzió eltér faktorral diszperziót, vagyis Ez egy torzított becslést a lakosság szórás. Ez annak a ténynek köszönhető, hogy ahelyett, hogy a valódi érték
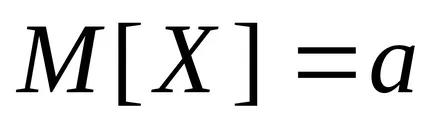

Ezért be egy felülvizsgált statisztikai szórás
Ezután a várakozás felülvizsgált statisztikai szórás egyenlő
azaz korrigáljuk statisztikai eltérés torzítatlan becslése a lakosság szórás. Az így kapott becslés is összhangban.