Euklideszi szerkesztés - az
Euklideszi szerkesztés
Szerkezetek vonalzó és iránytű - részén euklideszi geometria. ősidők óta ismert. A feladatok az épület egy iránytű és vonalzó használata ideális eszközök különösen:
- A sorban nincs megosztottság és van egy arc, végtelen hosszúságú, de csak egy.
- Az iránytű lehet tetszőlegesen kicsi vagy nagy önkényesen oldatban (azaz levonhatjuk egy tetszőleges kör sugara).
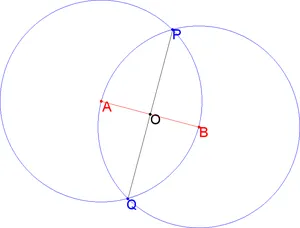
Hasadást fél hosszúság
A kihívás a kettéosztott. A rendszer segítségével egy vonalzó és iránytű felosztják a szegmens AB két egyenlő részre. Az egyik megoldás az alábbiakban mutatjuk be:
- Tájolók tart egy kör középpontja az A és B pontok AB sugárral.
- Keresse meg a metszéspontok P és Q két beépített körök (ívek).
- Lefolytatva vonalszakasz vagy áthaladó vonal pontok P és Q.
- Találunk a szükséges középpontját AB - AB metszéspontja és PQ.
A hivatalos meghatározás
A feladatok épület tartják a készlet minden pont a síkon, a sík meg az összes vonalak és a készlet minden körökben a sík, amelyen a következő műveletek engedélyezettek:
- Válasszon ki egy pontot a sor minden pontot:
- tetszőleges pont
- tetszőleges pont az adott vonalon
- tetszőleges ponton az előre meghatározott kerülete
- A metszéspont két egyenes
- metszéspont / érintés adott vonal és egy adott kör
- metszéspontján / contact két kör adott
- „A rendszer segítségével a vonalzó” kiosztani közvetlenül a készlet minden sorokat:
- önkényes vonal
- egy tetszőleges átmenő egy adott pont
- egy egyenes, amely átmegy a két megadott pont
- „Segítségével egy iránytű” fénypontja kerülete több körök:
- önkényes kör
- tetszőleges kör középpontja egy előre meghatározott ponton
- tetszőleges sugarú kör megegyezik a két pont közötti távolság
- középpontú kör egy adott ponton, és amelynek sugara egyenlő a két pont közötti távolság
Ami a probléma egy ponthalmaz. Szükséges egy véges számú műveletek számának megengedett műveletek fent felsorolt építésére egy másik ponton elhelyezett, egy előre meghatározott arányban a kezdeti beállított.
Megoldás épületben három alapvető részből áll:
- A módszer leírása építésének egy adott készlet.
- Igazolása, hogy a beállított leírt felépítésű, valóban egy előre meghatározott arányban a kezdeti beállított. Jellemzően az építési bizonyítási termelődik, mint a normál igazolást a tétel alapján axiómák és egyéb tételek bizonyult.
- Elemzés a leírt módszert alkalmaztuk annak alkalmazhatóságát a különböző kiviteli alakjai, a kezdeti feltételek, valamint a nem-egyediségét egyediségét vagy oldatok nyerhető ismertetett.
ismert probléma
- A probléma az építési Apollonius kör érintése három előre meghatározott kerülete van. Ha nincs a megadott kör nem hazudik a másik belsejében, ez a probléma 8 lényegesen eltérő megoldásokat.
- A feladat építésének Brahmagupta négyszög felírva négy oldala.
Építő szabályos sokszögek

Építése egy szabályos ötszög
Antik geométerek volt ismert módszerekkel építésének szabályos n -gons a ,, és.
1796-ban, Gauss megmutatta a lehetőséget az épület helyes n -gons mikor, hol - különböző prímszám Farm. 1836-Pierre Wantzel bebizonyította, hogy más szabályos sokszögek, amelyek által konstruált vonalzó és iránytű, nem létezik.
megoldatlan problémák
Az alábbi három építési kerültek az ókorban:
- Harmad szög - tetszőleges szöget szét három egyenlő részre.
- Duplázókocka - építeni egy kocka éle kétszer több, térfogat, mint a kocka
- A kör négyszögesítése - építésére egy négyzet egyenlő területű ennek a körnek.
Csak a XIX században bebizonyosodott, hogy mind a három probléma megoldhatatlan kizárólag vonalzót és iránytű. Kérdésre a lehetőséget az épület teljesen megoldható algebrai módszerek alapján Galois-elmélet.
- Egy másik híres megoldhatatlan segítségével iránytű és vonalzó feladat -, hogy építsenek egy háromszög három szögfelezői meghatározott hosszúságú. [1] Ezen túlmenően, ez a probléma továbbra is fennáll, még a jelenlétében trisektora. [2]
Lehetséges és lehetetlen, hogy építsenek
Minden konstrukciók nem más, mint a döntések minden egyenlet. amelyben az együtthatók az egyenlet társított előre meghatározott szegmensek hossza. Ezért célszerű beszélni az építőiparban - a grafikus megoldása az egyenletnek egy bizonyos típusú. Ennek része a fenti követelményeknek, az alábbi konstrukciót:
Más szavakkal, lehetőség van arra, hogy létrejöjjön egy számot egyenlő a aritmetikai kifejezések, a négyzetgyök felhasználásával a bemeneti számok (szakaszhosszok). Például,
- Ha csak egy szegmense hosszúságú, lehetetlen elképzelni ebben a formában (ezért lehetetlen a duplázó kocka).
- Lehetőség, hogy építsenek egy szabályos 17-szög következik koszinusza szög:
Variációk és általánosítások
- Szerkezetek egyetlen iránytű. A tétel Mohr - Mascheroni egy iránytű, meg lehet építeni bármilyen alakú, hogy meg lehet építeni egy körző és vonalzó. Ha ez tekinthető építendő egyenes, ha két pont van beállítva rajta.
- Épült ugyanabban a sorban. Ez könnyű észrevenni, hogy az egyetlen projektív invariáns építési végezhetjük egyetlen vonallal. Különösen lehetetlen még megosztani a szegmens két egyenlő részre, vagy megtalálni a központ a rajzolt kör. De a jelenléte a sík előre végzett egy kört központ jelölt vonalzó lehet ugyanolyan felépítésű, mint az uralkodó és iránytű (Poncelet tétel -. Steiner (angol)), 1833. Ha a vonal két fokkal, a szerkezet segítségével a ekvivalens konstrukciók vonalzóval és iránytű (fontos lépés bizonyítása, hogy Napoleon tette).
- Épült a fogyatékkal eszközöket. A problémák az ilyen típusú eszközök (szemben a klasszikus megfogalmazása a probléma), akkor nem ideális, de korlátozott: egyenest a két pont egy vonalzóval végezhetjük csak azzal a feltétellel, hogy a távolság két pont között nem haladja meg egy bizonyos értéket; sugara körök végzett mérőkörzővel korlátozott lehet a felső, alsó, vagy mind a felső és alsó.
- Az épület lapos origami. cm. Hudzita szabályok
érdekes tények
- A zászló minta le Iráni építési egy vonalzó és iránytű [3].
- Dynamic Geometry alkalmazás lehetővé teszi, hogy építeni a vonalzót és iránytű a számítógépen.