Fák orientált, rendezett és bináris

Fa - egy grafikon, amelyet az jellemez, a következő tulajdonságokkal:

1. Létezik egy különleges elem (node ​​vagy vertex), amely nem utal semmilyen más elemet -, és amely az úgynevezett gyökér.

2. Elején a gyökér és a következő egy bizonyos lánc mutatókat tartalmazza az elemeket, akkor lehet hozzáférni bármely szerkezeti elem.

A név „fa” származik a logikai ekvivalencia a fa struktúra absztrakt fa gráfelmélet. A kommunikációs kapcsolatot egy pár csomópont a fa ágai általában nevezik. Azokat a csomópontokat, amelyek nem utalnak más csomópontok a fa, az úgynevezett egy levél (vagy végpont) csomópont, amely nem egy levél, vagy root, úgy vélik, hogy egy közbenső csomópont vagy egy ága (vagy nemterminális belső vertex).

Egy irányított gráf az élek számát származó néhány kezdeti vertex V, az úgynevezett outdegree e csúcsból. Az élek száma, melyek a csúcs V véges, az úgynevezett-foka vertex V, és az összeg outdegree és beállítási csúcsok V úgynevezett teljes mértékben a tetején.

A következő kerül bemutatásra, hogy egy fontos osztályát grafikonok - orientált fák - és a megfelelő terminológiát. Fák kell ismertetni szerkezet egy hierarchia. Hagyományos példák ilyen szerkezetek: családfák, tizedes osztályozási könyvek a könyvtárakban, a hierarchia pozíciók a szervezeten belül, egy algebrai kifejezés magában műveleteket, amelyek bizonyos meghatározott elsőbbségi szabályokat.

Orientált fa - olyan gyűrűs, irányított gráf (digráf), amelyben az egyik csúcsa az úgynevezett gyökér, az a-foka 0, és a fennmaradó --foka 1. Egy orientált fát kell legalább egyik csúcsa. Az izolált csúcs is orientált fa.

Vertex-alapú fa outdegree amelyek nulla, ez az úgynevezett END (szuszpenzió), vagy csúcsa a lap; az összes többi csúcsai a fa egy ága csúcsot. A hossza a gyökér a vertex nevű SZINT (réteg szám) E csúcs. fa alapú gyökér szintű egyenlő nullával, és a szint a bármely más csúcs a távolság (azaz a különbség abszolút számok a csúcsok szintek) közötti ez a csúcs és a gyökér. Orientált fa aciklikus gráf, egészen benne elemi.

Sok alkalmazásban, a relatív sorrendje a csúcsok minden réteg egy konkrét jelentése. Amikor a fa nézet a számítógép automatikusan bekerül egy ilyen sorrendben, akkor is, ha maga önkényes. A sorozat a csúcsok egy bizonyos szint, akkor könnyen meg, a jelölés egyik csúcsa, mint az első, a másik - a második stb Ahelyett, hogy elrendeli a csúcsok megadhatja a sorrendben a széleit. Ha orientált fa minden szinten kap az, hogy a csúcsok, mint egy fa egy rendezett fa.

Azt is be néhány, a fogalmak kapcsolódó fák.

Csomópont X nevezzük őse (vagy apa), és Y és Z jelentése az úgynevezett csomópontok örökös (vagy fia) közöttük rendre nevezzük testvérek. És a bal oldalon van a fia a legidősebb fia, és a jobb oldalon - a legfiatalabb. A több részfák egy adott csúcsban az úgynevezett fokú csúcsok. (Ebben a példában, X jelentése 2 részfája így DEGREE vertex X jelentése

Ha a gyökér a fa, és távolítsa el a bordák kötik össze a gyökér a csúcsai az első szint, akkor kap egy csomó független fák. A készlet az úgynevezett erdei fák kötetlen

Láttuk, hogy a szekvenciák és listák lehet meghatározni, hogy megosszák a következők: bármely olyan szekvencia (spin-juice) egy bázissal típusú T - ez vagy:

üres szekvenciát (lista); vagy

konkatenáció (lánc) az elemek, és a szekvencia a T átáramló mennyiséget bázis típusú T.

Itt, a meghatározás strukturáló elvek (következőképpen vizsgálat vagy egy-iteráció) segítségével rekurzió. Miután a iteráció és olyan gyakoriak, hogy ezek általában Sí- olvadó alapvető „kép”, mint adatstruktúrák és a „menedzsment” programok. Azonban, ha mindig emlékezni, hogy a rekurzió csak akkor lehet meghatározni, de lyat rekurzió lehet hatékonyan és elegánsan használja a kádat meghatározása bonyolultabb szerkezetek.

Egy jól ismert példája a fák. Let vovidnaya-mag struktúra meghatározása a következő: a mag-vovidnaya bázis típusú szerkezet T - vagy:

1) egy üres szerkezetet; vagy

2) összeszerelése a T típusú, amely kapcsolatban van egy véges számú fa-szerű struktúrák-CIÓ bázissal típusú T-nevezett kíváncsiskodó revyami.

A hasonlóság a rekurzív definíciók következetesen stey és fastruktúrák Látható, hogy a szekvencia (lista) egy fa struktúra, amelyben minden egyes csomópont legfeljebb egy „részfa”. Ezért a követő-ség (a lista) is nevezik degenerált fa.

Vannak különböző módon fastruktúra képet. Tegyük fel például, a bázis típusától T egy sor betű; ez a fa struktúra különböző módon izo keményforrasztás ábrán. Mindezen gondolatok bizonyítják azonos szerkezetű, ezért egyenértékű. A pomoschyugrafa lehet szemléltetni az elágazási kapcsolatok érthetően vezetett obscheupotrebitel-Term kifejezés „fa”. Ugyanakkor furcsa módon, de a fák döntött festeni fejjel lefelé, vagy - ha az egyik inkább kifejezni ezt a tényt másképp -, hogy képviselje a fa gyökerei. De az utóbbi készítmény félrevezető, mint a felső csomópont (A) általában nazyvayutkornem. Bár mysoznaem hogy a természet a fák nem-sokkal bonyolultabb struktúrákat, mint a kivételi, akkor további fa szerkezet az úgynevezett egy fa.

Rendezett fa - egy fa, amely kazh-Dogo csomópont megrendelt ágak. Ennek következtében a két megrendelt kormányzati fa- is különleges, eltér más fák. Y csúcs, amely közvetlenül a X csomóponton nevezzük (közvetlen) leszármazottja x; Ha L naurovneI, mondjuk chtou - a urovnei - \ - \. Éppen ellenkezőleg, az úgynevezett uzelh (közvetlen) őse honnan. Úgy véljük, hogy a gyökér a fa található az 1. szinten Maxi-mal szint minden eleme a fa hívják mélysége vagy magassága.

Ha az elem nincs leszármazottai nevezzük terminális tag vagy övelemlap és egy nem-terminális, nazyvaetsyavnutrennim csomópont. Száma (Nepo-sredstvenno) leszármazottak belső nevű csomóponton egostepenyu. A legnagyobb mértékű, minden csomópont egy erő de-üvöltés. A fiókok száma, vagy a szélek, hogy kell eltelnie, hogy mozgatni a gyökértől a uzluh, nazyvaetsyadlinoy .Koren útvonalnak van egy olyan útvonal hossza 1, közvetlen leszármazottai - .. 2 úthossz, stb Általában, a csomópontot a szinten I módosulat úthossz Az L hossz fa meghatározása a hosszúságok összegét pu-mekek valamennyi egység. Úgy is nevezik, a hossza belüli ez így. Például, a hossza a belső fa utat ábrán látható. 2.1, egyenlő 52.

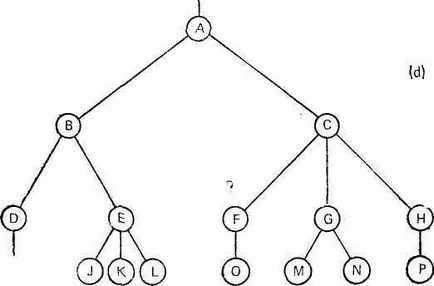
Ábra 2.1.Predstavleniya fa struktúra.

Annak érdekében, hogy meghatározzák az úgynevezett hossza extrinsic útvonal, akkor kiegészíti egy speciális facsomópont valahányszor vstre-chaetsya nulla részfa. Ugyanakkor úgy véljük, hogy az összes csomópont kell azonos mértékben - a mértéke a fa. Track-képpen ilyen kiterjesztése a fa magában kitöltő üres ágak, természetesen a speciális egységeknek nincs további leszármazottai. A fa ábrán látható. 2.1, komplement-nennoe speciális csomópontok, ábrán látható. 2.3, ha az SPE-sen csomópontok által képviselt négyzetek.

Ábra. 2.2 Két különböző bináris fa.

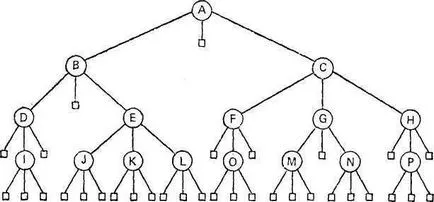
Ábra. 2.3. Hármas fát különleges csomópontokat.

A hossza a külső útvonal most összegeként definiáljuk dlinputey összes különleges egységek. A fa, ábrán látható. 2.3, a hossza a külső útvonal 153 egyenlő.

A számos speciális csomópontok m hozzá kell adni a fa foka d, közvetlenül függ az n szám-Khodnev csomópontok. Vegyük észre, hogy minden csomópont jelzi pontosan egy ága. Következésképpen, van egy expandált részfája m -f- n ágak. Másrészt, az egyes forrás csomópont d ágazik ki és a speciális csomópontok - audio. Ebben minden ág imeetsyadn -f 1 (1 engedélyezi ág, rámutatva, hogy a gyökér-vezető). Ezekből két egyenletet, megkapjuk a következő egyenlőség jelen-m közötti a számos speciális alkatrészek és n-TION kezdő csomópont: dn + 1 = m -f- n, vagy

A maximális száma a fa csúcsainak előre meghatározott magasságban H, megvalósítható abban az esetben, ahol minden csomópont d részfák kivéve szint H, nélkül csomó. Ezután, a mértéke d fa az első szinten 1 tartalmaz egy csomópontot (root) d level2 tartalmazza annak a gyermekek, 3. szint tartalmazza a gyerekek d2 d Tier 2 csomópont, stb Ez adja a következő érték ..:

azt a maximális számát a csomópontok egy fa h magassággal, és egy bizonyos fokú d. D = 2 jutunk

Rendezett fák mértéke 2 különösen fontos szerepet. Ezek az úgynevezett bináris fák. Mi határozza meg egy rendezett bináris fa egy véges elemekre, rendőrök (csomópontok), amelyek mindegyike üres vagy sostoitiz gyökér (node) csatlakoztatott két különböző binarnymiderevyami, az úgynevezett jobb és bal részfa a gyökér. A következő bekezdésekben az e szakasz, úgy véljük, csak bináris fák és miért fogyasztunk-lyat szó „fa”, azaz „egy rendezett bináris fa.” Fák, amelynek mértéke nagyobb, mint 2, nevezzük erősen elágazó fák (multiwaytrees). .

Ismerős példák bináris fák egy család (családi) fa apjával és az emberi anya, mint az ő leszármazottai, a történelem, a tenisztorna, ahol minden csomópont egy játék által meghatározott győztes, és részfák - az előző két játék ellenfelek (!); aritmetikai kifejezés kettős műveletek, ahol kazhdayaoperatsiya egy elágazási csomópont operandusokat részfákat.