fordítottja
Inverz arányossági egy funkcionális kapcsolat, amelyben a csökkenése vagy növekedése többször a független változó (argumentum) termel arányos növekedését vagy csökkenését a függő változók (jellemzők).
ahol k-akárhány, k ≠ 0.
Tegyük fel, hogy mi jön a boltba notebook. Notebook a pultra, és a pénzt a tárcájában fordítottan arányosak. Ie Minél többet vásárolni a notebook, a kevesebb pénz lesz.
Grafikon egy hiperbola.
Ütemezés funkció CFE> 0
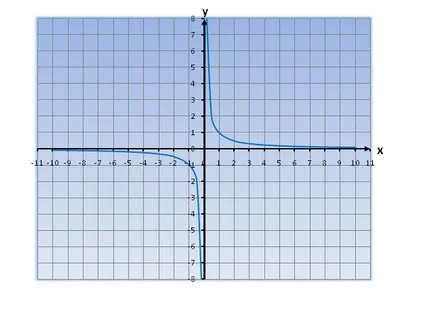
A hiperbola két részből áll: az egyik tárolja a negyedek I, ahol a pozitív értékek az X és Y, és a második rész - III negyedekbe, ahol az értékek a X és Y jelentése a negatív.
Ha megy az egyik ága a hiperbola származó -∞ és 0, megjegyezzük, hogy a működése csökken, mint az egyik mozog a másik ága a hiperbola 0 + ∞. aztán megint, azt látjuk, hogy a működése csökken. => Function. ahol K> 0. csökken.
Ütemezés funkció CFE<0

A hiperbola két részből áll: az egyik negyede 2, ahol a negatív értékek X és Y értékek a pozitív, és a második rész - az 4/4, ahol a pozitív értékek X és Y értékek negatívak.
A függvény pozitív érték az intervallumon (-∞; 0),
A függvény negatív értéket a (0; + ∞).
Ha megy az egyik ága a hiperbola származó -∞ és 0, tudomásul vesszük, hogy a függvény növekszik, mint az egyik mozog a másik ága a hiperbola 0 + ∞. aztán megint, azt látjuk, hogy a funkció növeli. => Function. ahol K<0. Возрастает.
1) a domain a funkció:
2) terület értékek:
3) a maximális és minimális értékek nem engedélyezettek a funkció.
4) - páratlan függvény (mert).
A grafikon szimmetrikus a származási (0, 0).
5) Ez a funkció nem korlátozott.
6) függvény nem metszi a koordináta tengelyek (OX és Oy).
Ha egy konstans (ahol a tetszőleges számú) a nevezőben kifejezést, mint X. mozgás fog bekövetkezni tengelye körül a hiperbola X (együtt a függőleges aszimptotával).
Ebben az esetben az egyenlet a függvény a következő lesz:
Ha van egy „+” jel (). A függvény grafikonját mozog oX tengelyen a bal oldalon.
Vegyük például az egyenlet
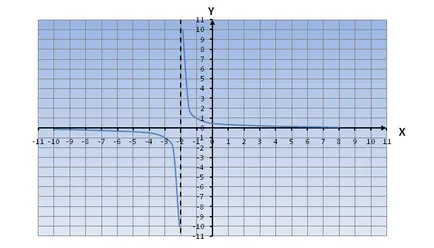
Hiperbola eltolt 2 balra.
Ha van egy „-” jel (), a függvény grafikonját mozog oX tengelyen jobbra.
Vegyük például az egyenlet
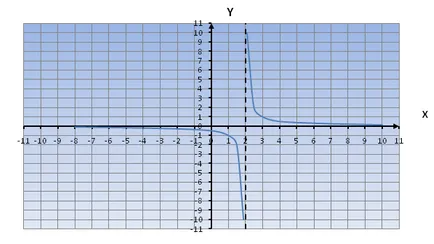
Túlzó eltoljuk 2 jobbra.
Ha ehhez hozzátesszük a konstans b (ahol b tetszőleges számú), hogy frakció, mint egy összeadandó, nem lesz mozgását a hiperbola oY tengely (a vízszintes aszimptotával)
Ebben az esetben az egyenlet a függvény a következő lesz:
Ha b egy „+” jel (), a függvény grafikonját mozog oY tengelyirányban felfelé.
Vegyük például az egyenlet
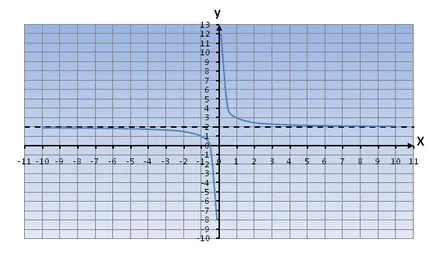
Ha b egy „-” jel (), a függvény grafikonját mozog oY tengelyen lefelé.
Vegyük például az egyenlet

A hiperbola tolódik le 2.
Leszűkítése és bővül a menetrend tekintetében a származás.
A K együttható függ, hogyan viselkednek hiperbola képest az eredetét.
Például, hasonlítson és.
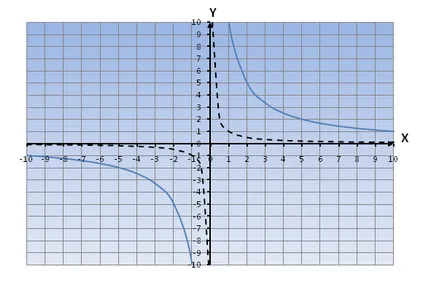
Látjuk, hogy a függvény grafikonját sokkal szűkebb, mint a grafikon => Minél magasabb a K együttható, annál nagyobb a távolság az ágak között túlzás a származás.
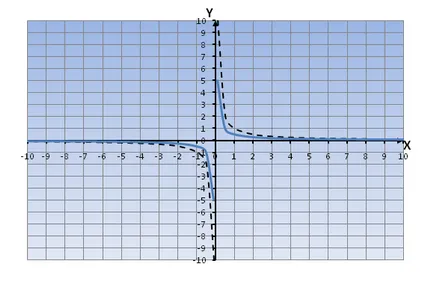
Látjuk, hogy a függvény grafikonját sokkal szűkebb, mint a grafikon => Minél kisebb a K együttható, annál kisebb a távolság az ágak között túlzás a származás.