Fuzzy száma 4
4.1 A koncepció a fuzzy számát
Fuzzy száma - ez fuzzy változók a valós tengelyen, más szóval, a fuzzy szám meghatározása a fuzzy halmaz

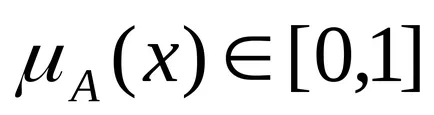
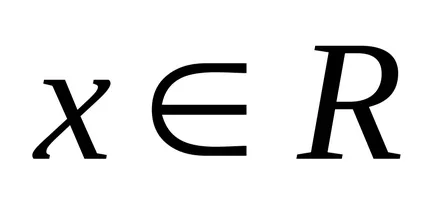
Fuzzy számot hívják normális. ha konvex. ha bármilyen
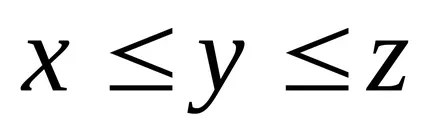
.
sok


.
részhalmaza
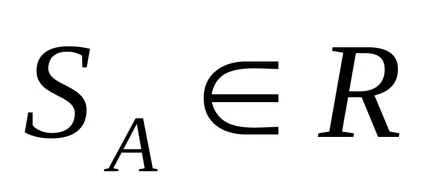

.
Unimodális fuzzy szám. ha a feltétel
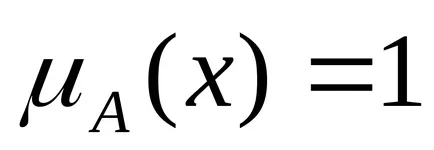
Konvex fuzzy számot hívják fuzzy nulla, ha
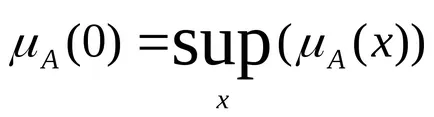
Fuzzy szám pozitív. ha

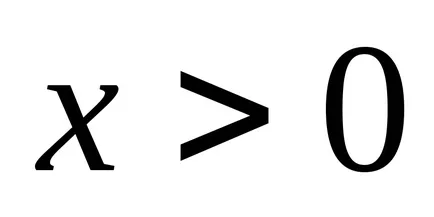

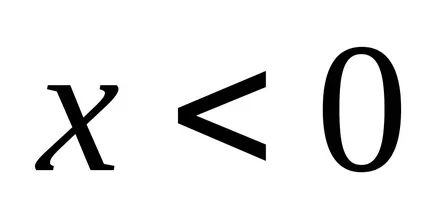
4.2 Műveletek fuzzy számok
Bővített bináris aritmetikai műveleteket (. Összeadás, szorzás, stb) a fuzzy számok meghatározni a megfelelő műveleteket, hogy egyértelmű számok segítségével általánosítása elvének az alábbiak szerint:
Használd így meghatározott algebrai műveletek fuzzy számok nem praktikus, mert a nagy mennyiségű számítási. Ezért gyakran használják a képviselete fuzzy számok
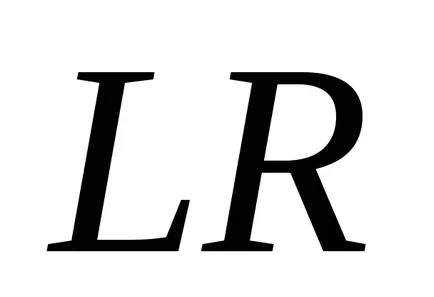
Fuzzy száma
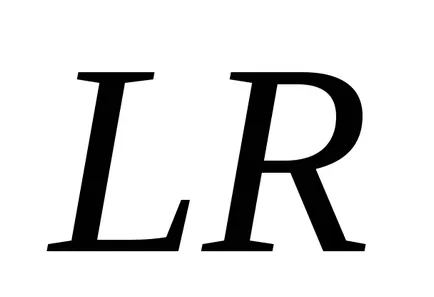
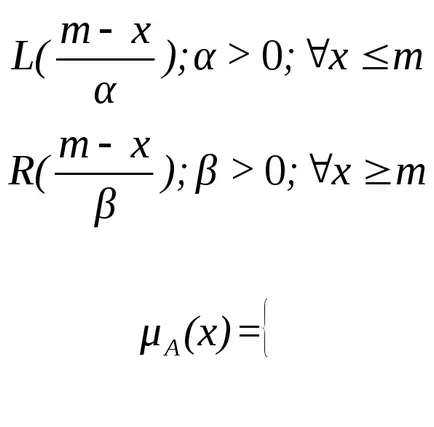
ahol
,
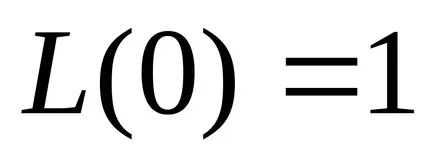
függvény
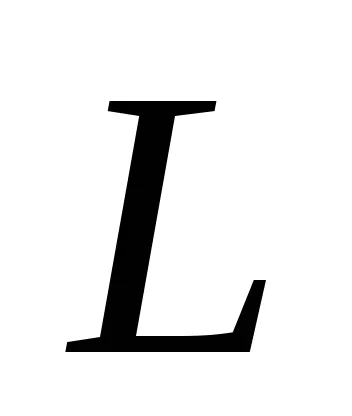
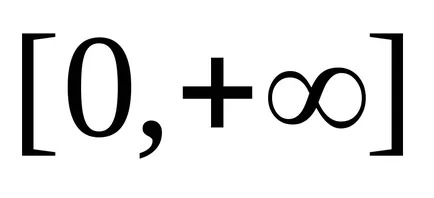
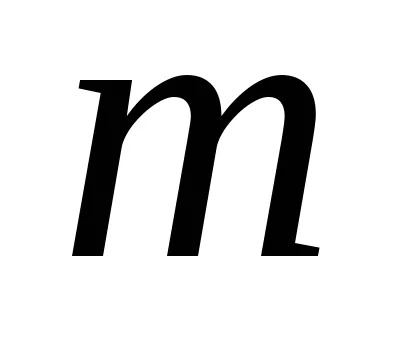





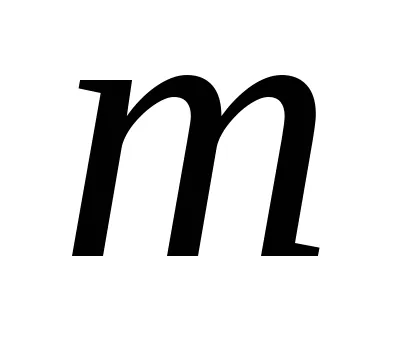
Így egy fuzzy szám
gyakorlatban
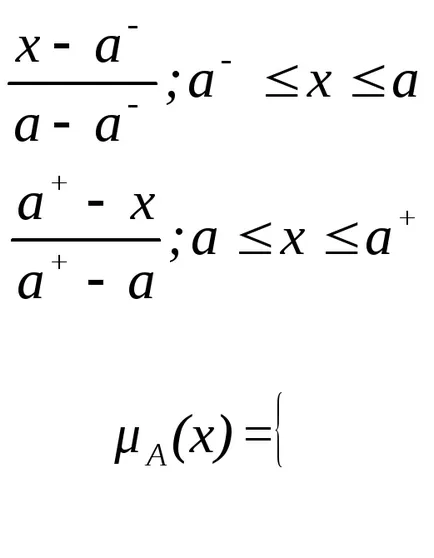
Sőt, elterjedése trapéz alakú tagsági függvényeket, amelyek a forma
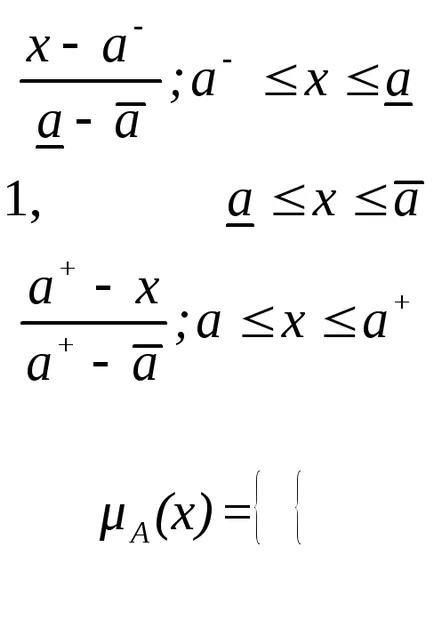
A megoldás a problémák matematikai modellezése a komplex rendszerek fuzzy halmazok igényel nagy mennyiségű műveletek különböző nyelvi és más fuzzy változók. Az egyszerűség kedvéért a műveletek, valamint az IO és tárolás, kívánatos, hogy működik a funkciók normál típusú kiegészítőket.
Sajnos, még a csökkentés fuzzy számok fogalmának háromszögszámok, továbbra is megoldatlan probléma az ellenkezőjét, és fordított elemek és a forgalmazás és ingatlan. Egy másik jelentős hátránya ennek a megközelítésnek. Blur, a termék nem csak attól függ a blur tényezők, hanem az elfoglalt helyére adatok fuzzy számok a valós tengelyen. Tegyük fel például,
A = (1, 2, 3), B = (2, 3, 4), majd AB = (2, 6, 12)
és C = (99, 100, 101), az E = (100, 101, 102),
ha CE = (9 900 10 100, 10 302).
Ebből a példából következik, hogy az Európa Tanács több homályos, mint az AB.
Fuzzy halmazok kell használni a legtöbb feladatot általában unimodális és normális. Az egyik lehetséges megközelítési módszerei fuzzy halmazok unimodális közelítés alkalmazásával