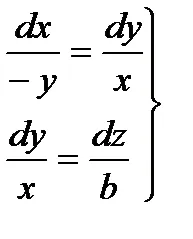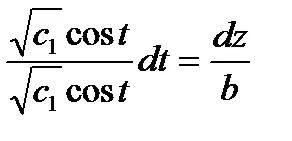gradiens tulajdonságok - studopediya
1 0 A gradiens mentén irányul normális a felszíni szinten (vagy olyan szintre vonal, amikor egy mező lapos).
2 0 A gradiens irányul irányába növekvő mező funkciót.
3 0 A gradiens modul legtöbb származéka napravleniyuvdannoy pont mezők:
Ezek a tulajdonságok teszik egy invariáns gradiens jellemző. Azt mondják, hogy fokozatosan vektor irányát jelzi, és nagysága a legnagyobb változások a skalármező egy adott ponton.
Megjegyzés 2.1. Ha a függvény U (x, y) függvény a két változó, a vektor
Ez síkjában az oxi.
Legyen U = U (x, y, z) és V = V (x, y, z) differenciálható a ponton M0 (x, y, z) függvény. Aztán ott van a következő egyenletek:
a) grad () =; b) grad (UV) = VgradU + UgradV;
a) grad (U V) = fokozatosan gradV; g) g) Grad =. V;
d) fokozatosan (= fokozatosan, ahol. U = U () van egy-származék.
Példa 2.1. Adott funkció U = x 2 + y 2 + z 2. Határozzuk meg a gradiens a függvény az M pont (-2, 3, 4).
Határozat. Szerint egyenlet (2.2)
,
.
Szint felületei skalármező egy család gömbök x 2 + y 2 + z 2. vektor fokozatosan = (- 4; 6; 8) egy normális vektor síkok.
Példa 2.2. Find a gradiens egy skalármező U = x-2y + 3Z.
Határozat. Szerint egyenlet (2.2)
Level felületei skalármező síkok
X-2y + 3z = C; vektor fokozatosan = (1, -2 és 3) van egy normális vektor a család síkok.
Példa 2.3. Megtalálni a maximális felületi lejtő U = x y pontban M (2; 2; 4).
Példa 2.4. Találja a készüléket vektor felületre merőleges szintjét skalármező U = x 2 + y 2 + z 2.
Határozat. vízszintes felületen a belső-gömb Fields x 2 + y 2 + z 2 = C (C> 0).
A gradiens a normális, hogy a sík felületre úgy, hogy
. Meghatározza egy vektor merőleges a réteg felületére egy ponton M (x, y, z). Ahhoz, hogy a készülék vektor normális expressziós
.
Példa 2.5. Find a gradiens U =. ahol a konstans vektorok, r a sugár vektor egy pont.
majd:
Példa 2.6. Keresse meg a gradiens a távolságot. ahol P (x, y, z) - vizsgált területen pont, P0 (x0, y0, z0) - egy fix pont.
Határozat. Van - egységvektor irányában.
Példa 2.7. Find közötti szög gradiense a függvény a ponton M0 (1,1).
Határozat. Találunk színátmenetek ezeket a funkciókat a ponton M0 (1.1), van
; A bezárt szög fokozatosan és gradV egy pont M0 következő egyenletből meghatározzuk
Példa 2.8. Megtalálni a származék az irányt a sugár vektor
Határozat. Találunk a gradiens ezt a funkciót:
Behelyettesítve (2.5) a (2.4) a hozamokat
Példa 2.9. Megtalálni azt a pontot M0 (1, 1, 1) irányában a legnagyobb változást a skalármező U = xy + yz + xz és nagyságát a legnagyobb változás ezen a ponton.
Határozat. A legnagyobb változások által jelzett irányba a vektor mező grad U (M). Úgy találjuk, hogy:
És akkor. Ez a vektor irányát határozza meg legnagyobb növekedést a mező ponton M0 (1; 1; 1). Nagysága a legnagyobb változás a területen ezen a ponton megegyezik
.
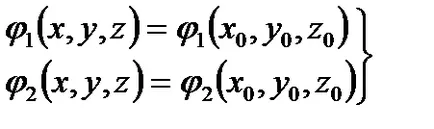
Példa 3.1. Keresse meg a vektor vonalak egy vektor mező, amely egy állandó vektor.
Határozat. van olyan
Differenciálegyenletek vektor vonalak
Szorzás a számláló és a nevező a frakció az első x, és a második Y-on, az utolsó csomag, és adjunk hozzá termwise z. Az arányok az ingatlan, megkapjuk
. így xdx + ydy + ZDZ = 0, amely eszköz
x 2 + y 2 + z 2 = A1. A1 -const> 0. Most szorozzuk meg a számláló és a nevező az első frakció (3.3) C1. második -on c2. harmadik c3, és az oldathoz Terminusonként megkapjuk
. ahol c1 dx + c2 dy + c3 dz = 0
Kötelező egyenletek vektor vonalak

Ezek az egyenletek azt mutatják, hogy a vektor vonalak az eredménye a kereszteződésekben a gömbök, amelyek közös központ a eredetű, merőleges síkban a vektor. Ez azt jelenti, hogy a vektor vonalak körök, amelyek középpontjai egy egyenesen átmenő eredetű az irányt a vektor. Körök merőleges síkban egyenes vonal.
3.2 példa. Keressen egy vektor erővonalán ponton áthaladó (1,0,0).
Határozat. Differenciálegyenletek vektor vonalak
így van