Ha ismerjük a gépet görbe
Tekintsünk egy tetszőleges folyamatos görbét AB. amelynek nincs önálló metszéspontjai. Ha minden ponton érintőjének M, ez mozgás közben TM A-ból B lesz elforgatva.
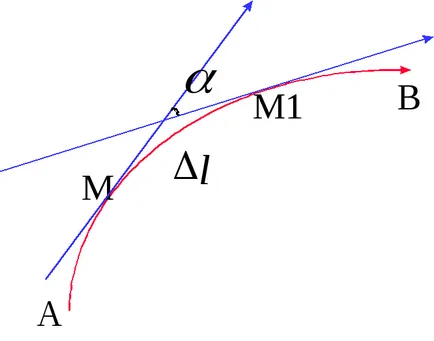
Ez a görbe különbözik egy egyenes vonal, ahol az érintő mindig ugyanaz, nevezetesen, egyesül egy egyenes vonal.
Minél gyorsabban fordul tangens, annál ívelt görbe, annál nagyobb a „görbület”.
Adunk egy matematikai definíciója görbületi íve. Tekintsünk egy tetszőleges ív MM1 azokon a pontokon, M és M1 magatartás nyírás. Tegyük fel, hogy a köztük lévő szög meg nazyv szög szomszédsági dugaMM1 = S. Ezután az arány / S említett. jelenti görbület görbe AB MM1 része. Az átlagos görbület jelzi a forgásszög mozgatásakor az érintési pontok M egységnyi hossza a görbe mentén. Különböző részein az átlagos görbület a görbe változik. Csak az egyik görbe - a közepes görbülete a kör állandó: DAC = / S = / (R) = 1 / R, azok a kör görbület a kölcsönös a sugara.
Ahhoz, hogy pontosan jellemezze a görbület a görbe azon a ponton görbületi koncepció kerül bevezetésre, jelölésére K.
A görbület a görbe TM nazyv limit (ha sesch-a), amely hajlamos arra, hogy íves görbületi MM1 táptalajra, amikor t.M1 görbe hajlamos M.
K = limS

Limit (1) nem más, mint a származék a dőlésszög az érintő a ív hossza, és ezért az utóbbi határérték egy határ, hogy az arány a növekmény funkciója a növekmény az érvelés, azaz származék: K = d / dS, (2).
Így, a görbület a görbe egy ponton a származék a hajlásszöge a érintője az ív hossza a görbe. Görbület száma nem negatív, így valójában K = | d / DS |, (2 „).
Tól képletű (2) megkapjuk egy kényelmes görbülete a gyakorlatban f lu, amikor a görbe meghatározása parametrikusan.
Tegyük fel továbbá, hogy a funkció (t), (t) folyamatosan a származékok megbízások az 1. és 2., valamint xt '= ' (t) t adott esetben TM
Aztán DS =, opredelimd.
d = helyettesítve DS, d a (2 „), hogy = |

Ha egyértelmű görbét az alábbi egyenlet adja y = f (x) feltételezzük, hogy a paraméter a t = x, akkor

Ha a görbe adott poláregyenlet , akkor feltételezzük, t = kapjunk

Példa. Határozza meg a görbület a görbe y = Sinh a TH = n / 2 -SAMOSTOYATELNO.
§3.Radius, a kör és a görbületi középpontja. A koncepció a evolután és evolvens.
Definíció: Az R érték, a fordított görbülete ponton kapott görbét K, nazyv görbületi sugara a görbe ezen a ponton: R = 1 / K. Közvetlen a görbületi sugár végtelen látnia e vonal egy kör végtelen sugarú.
A kerülete Radus krivizny- van a szokásos tartományban, görbék paraméteres formában adtuk vagy explicit egyenlet y = f (x) vagy görbületi sugara könnyen előállítható a képletű (3) - (5). Így y = f (x) R = 1 / K =, stb (saját).
Készítünk egy görbe tm normál hozzá és félretesszük konkáv szegmens MC = R.
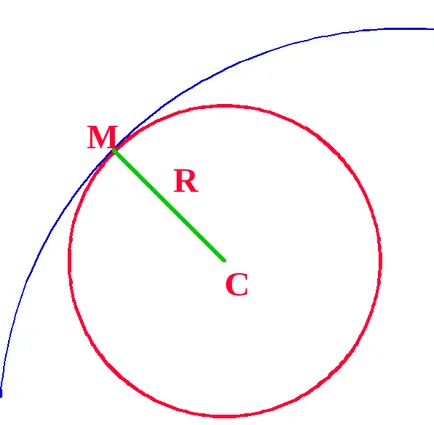
C pont nazyv a görbületi középpont a TM, egy kör (kör) középpontú C és R sugarú nazyv kör (kör) a sorban a görbületi TM A TM görbe és a görbület k kör nekik ugyanazt görbületét, így íves görbe közelében M egy kis hiba lehet helyettesíteni egy ív görbületének kör ezen a ponton.
Minden pont a görbe M (L) saját görbületi középpontja a C pont a TM
A lókusz a görbületi középpontok a görbe (L) nevezzük annak evolután (L „). (L „) - is vannak bizonyos görbe. Tekintettel (L „) eredeti görbe (L) nevezik evolvens vagy szkennelni. Ott formula. lehetővé téve a egyenlet a görbe (L), hogy írjon egyenlet evolután. És fordítva.
Szinte evolután e görbe lehet kialakítani a következőképpen. Belátható, hogy minden egyes merőleges a görbe (L) yavl. érinti a evolután. Ezért az épület elegendő számú normális hordani egy görbét, amely az összes ilyen normaley- boríték merőlegesek.
Evolvens az evolután van lehetőség, hogy mechanikusan.

Hagyja, rugalmas vonalzó hajlott elme evolután C C0 C0 tulajdonítanak a végén a menet szoros, és húzza a vonalon.
Ha ez a téma már telepített húzva minden alkalommal a szabad végén, akkor írja le egy görbe, amely evolvens görbe C. Mivel a C0 szálak hosszúsága eltérő lehet, a evolvensek egy evolután tetszőleges szám lehet.