Használatának korlátozása a teszt Durbin-Watson
csak akkor, ha a következő feltételek vonatkoznak a Durbin-Watson teszt:
A regressziós egyenlet legyen szabad tagja jelen van.
Kovariánsai nem-sztochasztikus.
A regressziós egyenlet nem késleltetett értékei a függő változó.
4. kimutatására használt autokorrelációs csak maradék közötti regressziós egymást követő megfigyelések. Például, ha, de aztán a Durbin-Watson teszt nem képes kimutatni autokorrelációs.
3. Az általánosított legkisebb négyzetek módszerével enyhítésére és felszámolására heteroszkedaszticitásra autokorrelációs
a) csökkentési heteroszkedaszticitás
Ha tudja, hogy az ok (és ennek megfelelően az alakja heteroszkedaszticitás), majd oldja meg a problémát, akkor az általánosított legkisebb négyzetek módszerével (OLS).
Feltételezve, hogy a szórás a regressziós maradékok kapcsolódó valamilyen függőség változó zt
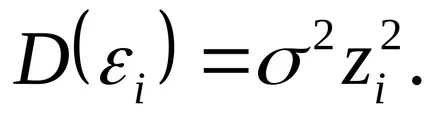
Mivel változó lehet:
1) szórás σt (ha ismert), ebben az esetben, egy eljárás súlyozott legkisebb négyzetek (WLS);
2) xi vagy
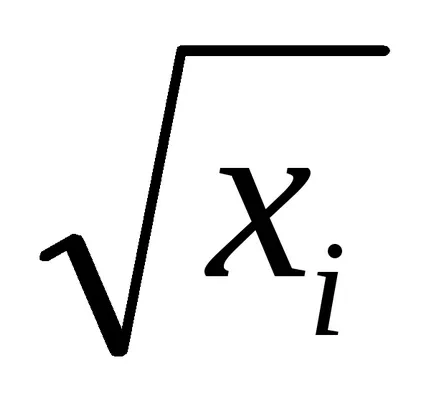
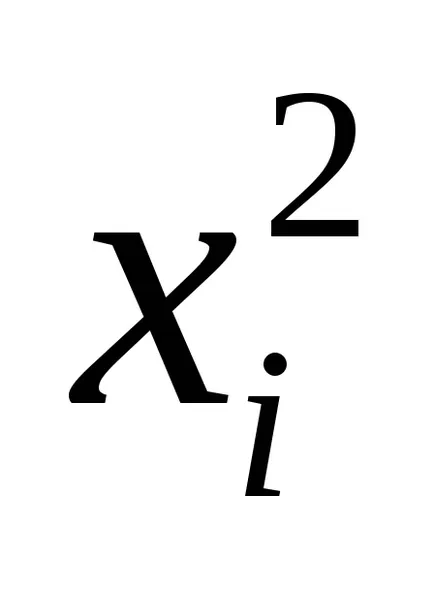
Annak érdekében, hogy megszabaduljon a heteroszkedaszticitás elosztja az egyes kifejezés a regressziós egyenlet
(*)
ahol
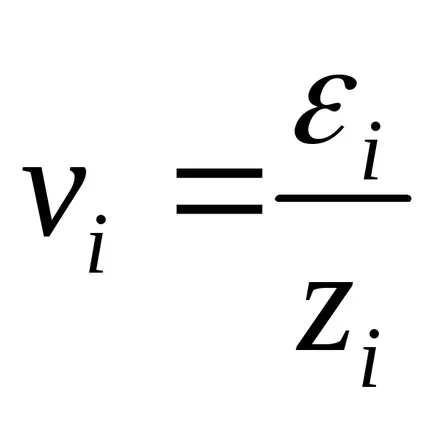
Így, a hiba egyenlet (*) vannak homoszkedaszticitás.
A gyakorlatban azonban ez gyakran nem lehetséges biztosan megállapítani, okait és formáit heteroszkedaszticitást. Ebben az esetben, akkor sem átvinni minden változót logaritmikus formában (de nem szabad elfelejteni, hogy ez a módszer nem alkalmazható, ha a változók a modell tudja fogadni nulla vagy negatív érték), vagy kihasználják a különleges robusztus értékelési módszerek.
b) megszüntetése autokorrelációs
Ahhoz, hogy megszüntesse a autokorreláció (például abban az esetben, heteroszkedaszticitás) használhatja a általánosított legkisebb négyzetek módszerével (OLS).
AR (1) modellként autokorreláció, írhatunk:
Feltételezve, hogy a modell szerkezete állandó, egy t időszak -1 kapjunk modell:
Szorozzuk egyenlet mindkét oldalát (2) a
