Hiperbola (a geometriában)

Hiperbola, metszésvonal egy jobbmenetű kúpot egy sík nem halad át a csúcsát a kúp és a metsző mind annak üreg (ábra. 1). A hiperbola is definiálható, mint a pontok helye síkban M, ami a különbség a távolság a két specifikus pont az F1 és F2 síkja (gócok a hiperbola) állandó. Ha úgy döntünk, az xy koordináta-rendszer a 2. ábrán látható (OF1 = OF2 = s), gierboly Az egyenlet:

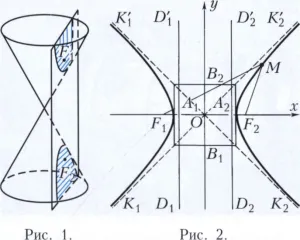
2a, ahol M = F1-F2 M, b = 2 -a √s 2. hiperbola - másodrendű vonal áll a két végtelenített ágak K1 és K2, K'1 A1 A2 k'2. ez szimmetrikus a tengelyek F1 F2 B1 és B2. O pont (közepén a hiperbola) van a közepén a szimmetria, a szegmensek A1 A2 = 2a, B1 B2 = 2b úgynevezett valós tengelyének és képzetes tengelyének a hiperbola hiperbola száma e = c / a> 1 - excentricitása a hiperbola. Közvetlen D1 D1 „és D2 D'2. egyenletek, amelyek X = -a / E és X = egy / e az úgynevezett directrices hiperbola, az arány a távolság a legközelebbi pont a hiperbola fókuszt a távolság a legközelebbi direktrix állandó és egyenlő excentricitás. A1 és A2 keresztezi Ox túlzás nevű csúcsához. Közvetlen y = ± bx / a (ábrázolt fantom 2. ábrán) - hiperbola aszimptotákkal. Graph fordítottan arányos y = k / X egy hiperbola. Lásd még kúpszeletek.

kapcsolódó cikkek

← hiperbola (az irodalomban)