Hogyan építsünk egy fraktál sor Apollo

2. rész 2: építése az Apollo szerkesztése

Sok Apollo formáját ölti egy szép fraktál design csökkenő ütemben kört. Matematikailag sok Apollo végtelenül bonyolult, de ha használ egy számítógépes program, vagy a hagyományos rajzeszközök, akkor előbb-utóbb eléri azt a pontot, ahol lehetetlen lenne, hogy dolgozzon egy kisebb kört. Megjegyezzük, hogy minél pontosabban rajzol egy kört, annál jobban megfeleljen a különböző Apollo.

Kezdjük egy nagy kört. Az első feladat - csak felhívni egy nagy, tökéletesen sima kör. Minél nagyobb a kör, annál nehezebb lehet a fraktál, így próbálja építeni egy kört, amely lehetővé teszi a papír méretét, vagy úgy, hogy azt teljes mértékben a képernyőn lát egy grafikai program.

Rajzolj egy kört kisebb az első körben, ami érinteni fogja ez egy ponton. Tehát, rajzoljon egy kört körön belül az első, akkor kevesebb lesz, mint a fő, de még mindig elég nagy. A pontos méret a második kör rajtad, mivel nincs fix összeg. Azonban nézzük felhívni a második kört úgy, hogy felveszi felében a fő kör. Más szóval, a közepén - ez a középső sugara nagyobb kört.

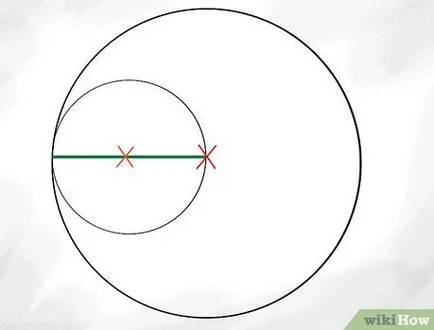
Megjegyezzük, hogy a beállított Apollo összes körök érintik egymást. Ha építése iránytű körökben újra ezt a hatást azáltal, hogy a hegyes vége egy iránytű közepén alapkör sugara, és beállítjuk a tájoló ceruzát úgy, hogy csak érinti a szélén a kör, majd rajzoljon egy kisebb belső kör.

Rajzolj egy kört közel azonos a belső kerületén. Úgyhogy felhívni egy másik kört az első mellé. A kör kell érintőleges mind körök: a legkülső és a belső, alsó, ami azt jelenti, hogy mind a belső kerülete szomszédosak pontosan a közepén nagy.

Alkalmazása az elmélet a Descartes, méretének kiszámításakor e körök. Egy pillanatra megáll rajz. Most, hogy megvan a három kör a fraktál, fel tudjuk használni Descartes-tétel, hogy megtalálják a sugara a következő kör, amely levonja. Megjegyzés Descartes-tétel egyenlet d = a + b + c ± 2 (√ (a × b + b × c + c × a)). ahol a, b, és c a görbülete három kör érintője és d - a görbület kör érintőleges mindhárom. Ezért, hogy megtalálják a sugara a következő fordulóban, nézzük kiszámítja a görbület minden a mi meglévő körbe, amíg találunk a görbület a következő kört, majd kiszámítja a sugara.

Nézzük meg a sugár a külső kerülete, mint 1. Mivel a más körökben helyezkednek el benne, van dolgunk „belső” görbült (ahelyett, hogy külső), ezért tudjuk, hogy az negatív. - 1 / r = -1/1 = -1. Mivel a görbület a nagy kör egyenlő -1.
A sugara kisebb kör fele a sugara a nagy, azaz 1/2. Mivel ezek a kerülete érintkezik egymással, és a fő kör Külsőleg, meg kell foglalkozni a külső görbület pozitív. 1 / (1/2) = 2. Ezért a görbület a kisebb kör egyenlő 2.
Most már tudjuk, hogy a = -1, b = 2 és c = 2 egyenletünk Descartes-tétel. Nézzük kiszámítja a d:
- d = a + b + c ± 2 (√ (a × b + b × c + c × a))
- d = -1 + 2 + 2 ± 2 (√ (-1 × 2 + 2 × 2 + 2 × -1))
- d = -1 + 2 + 2 ± 2 (√ (-2 + -2 + 4))
- d = -1 + 2 + 2 ± 0
- d = -1 + 2 + 2
- d = 3. A görbület a következő kerületileg 3. Mivel 3 = 1 / R, a sugara ebben a körben egyenlő 1/3.

Döntetlen a következő pár kört. Felhívni a következő két kört, a sugár, hogy éppen most találtam. Ne feledje, hogy ezek a körök érintőleges azoknak, akiknek a görbület volt kiszámítására használt derékszögű tétel. Más szóval, akkor érintse meg a primer és szekunder körében. Ahhoz, hogy ezek a körök megérintette a másik három, meg kell felhívni őket a nyílt terület felett és alatt a fő fordulóban.

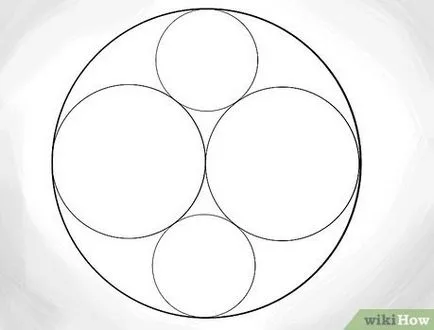
Megjegyezzük, hogy a sugár e körök egyenlő 1/3. Mérjük 1/3 külső kerületének peremén, majd felhívni egy újat. Meg kell érintő mindhárom kört a környéken.

Így folyamatosan hozzá kerülete. Mivel ezek fraktálok, sok Apollo végtelenül bonyolult. Ez azt jelenti, hogy felveheti a kör egyre kisebb a bázis a fraktál. Ön kizárólag csak a pontosságát a szerszám (vagy, ha használja a számítógépet, a képesség, hogy növelje a grafikai program). Minden kör, akármilyen kicsi is lehet, érintője kell legyen a másik három. Ahhoz, hogy rajzoljon egy kört minden ezt követő használata a görbület három kör érintője ez a tétel Descartes. Ezután a válasz pontosan dolgozzon egy új kört.

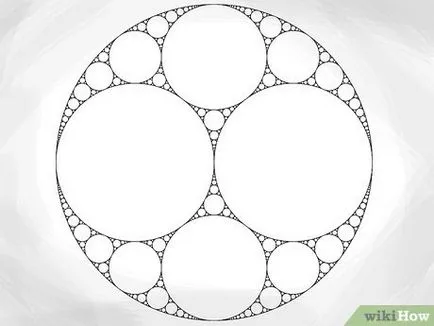
Megjegyezzük, hogy a halmaz, amely úgy döntöttünk, hogy épít, szimmetrikus, így a kör sugarát megegyezik a kör sugarát azonos vele. Azonban nem minden készlet Apollo szimmetrikus.
Nézzünk egy másik példát. Tegyük fel, miután az építése az utolsó pár kört, szeretnénk felhívni a kör érintője a harmadik párt, és az alapkör. A görbületi e körök jelentése 3, 2 és 1, illetve. Most ezeket a számokat derékszögű tétel, megállapítva, hogy a = -1, b = 2 és c = 3:
- d = a + b + c ± 2 (√ (a × b + b × c + c × a))
- d = -1 + 2 + 3 ± 2 (√ (-1 × 2 + 2 × 3 + 3 × -1))
- d = -1 + 2 + 3 ± 2 (√ (-2 + -3 + 6))
- d = -1 + 2 + 3 ± 2 (√ (1))
- d = 2, 6. Van két válasz! Tudjuk azonban, hogy az új kör kisebb lesz, mint az érintő, ezért csak akkor van értelme, hogy értékeljük a görbület 6 (a sugara 1/6).
- Egy másik válasz, 2, valójában egy hipotetikus kört a „másik oldalon” az érintő pont a második és a harmadik kör. Ez a kör érintője mind ezeket a köröket, és a fő, de ő majd át azokat a kör, amelyet az imént húzott, így figyelmen kívül hagyja ezt a választ.

Próbaképpen próbálja építeni egy aszimmetrikus szett Apollo, méretének megváltoztatásával a második kör. Minden készlet Apollo elkezdik építeni az azonos - egy nagy külső kerülete, amely a határ fraktál. Azonban nincs szükség, hogy megegyezzen a sugara a második kör első felében. Mi csak úgy döntött, hogy ezeket a számokat az egyszerűség és a könnyebb érthetőség. A szórakozás, próbálja meg felépíteni egy új, a második körben a különböző méretű - ez vezet az új irányok a kutatásban.

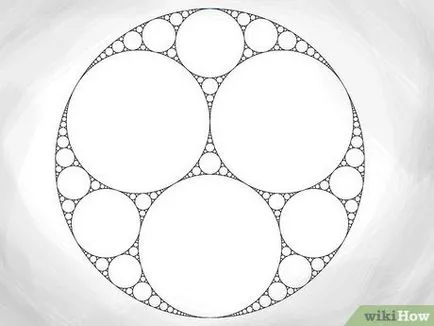
Amikor épült a második kör (méretétől függetlenül), akkor a következő intézkedéseket kell építeni egy (vagy több) a kör, hogy az érintő a második és a fő külső kerületének - nem csak a helyes módszer, hogyan kell építeni. Ezután használhatja a tétel a Descartes, hogy meghatározzuk a sugár a következő körökben, a fentiek szerint.