Hogyan kell felhívni a Koch hópehely fotó-rendszer úgy néz ki, mint a Koch hópehely
Koch hópehely -? Hogy ez a szám az egyik első tudós tanulmányozta fraktálok. Hópehely nyerik három példányban a Koch-görbe, tájékoztatás a felfedezés megjelent 1904-ben egy cikket a svéd matematikus Helge von Koch. Tény, hogy a görbe úgy került kialakításra, mint például egy folytonos vonal, amely lehetetlen felhívni a érintő vonal bármely pontján. Koch-görbe egyszerű a design.
Példa, fotó-rajz képek a Koch hópehely fokozatos rajz.
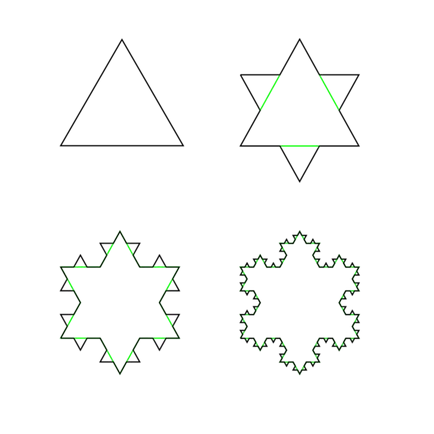
Ezen az ábrán látható vonalak részlet, ami később kiderül Koch hópehely.

És ez egy új értelmezése a hópelyhek alapján a Koch hópehely.
Kezdeni, úgy a Koch hópehely. A legjobb, hogy megmutassa az áramkör alább látható.
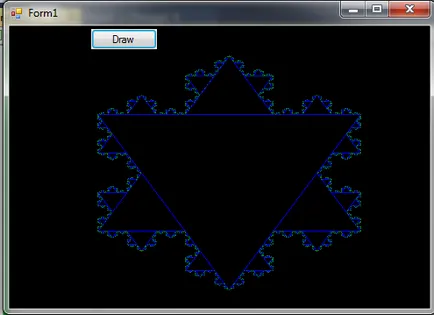
Azaz rajza hópelyhek kell használni az egyes geometriai formák teszik fel ezt a geometrikus fraktál.
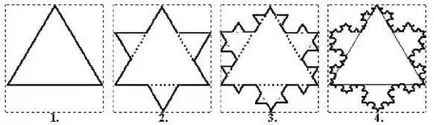
Alapja az a szám egyenlő oldalú háromszög. Mindegyik oldalon három szegmensre osztottuk, amelyek közül a következő, kisebb egyenlő oldalú háromszög épített. Az így kapott háromszög végezzük a műveletet, és így többször is.