Hogyan rajzoljunk a függvény grafikonját modul és a gyökér
Tekintsük az y = │ah │, ahol egy - egy bizonyos számot.
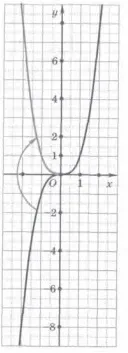
A domain a funkció y = │ah │, a valós számok halmaza. Az ábra azt mutatja, grafikonok rendre funktsiyu = │h │, y = │ │ 2, y = │h / 2│.
Talán észrevetted, hogy a grafikon y = | ah | nyert függvény grafikonját y = ax. ha a negatív része a grafikon y = ax (ez alatt az x-tengely), tükrözik a szimmetrikus tengely.
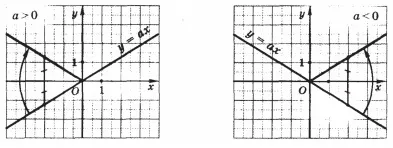
Az ütemterv szerint könnyen belátható a tulajdonságait a függvény y = ax │ │.
Ha x = 0, y = 0, megkapjuk, hogy tartozik a grafikon származási x = 0, y van> 0, azaz minden más grafikai pontot fölött fekszik az x tengely.
Az x értékek ellentétes. értékek azonosak legyenek; Y-tengely a szimmetria tengelye a grafikon.
Például, lehet építeni egy grafikon y = 3 │h │. Annak érdekében, hogy összehasonlítsuk a funkció y = │h │i 3 y = x 3 pótolni egy táblázatot az értékek az azonos értékeket érveket.
Tekintsük az y = x 1/2.
A tartomány ennek a funkciónak a készlet nem negatív valós számok, mivel a kifejezés x 1/2 értéke csak akkor, ha x> 0.
Készítünk egy grafikont. Ahhoz, hogy állítson össze egy táblázatot az értékeknek a számológép, a kerekítés a függvény értékei a tizedik.
Az alkalmazás után a pontokat a koordináta sík és sima azok vegyületei, megkapjuk a grafikon funktsiiu = x 1/2.
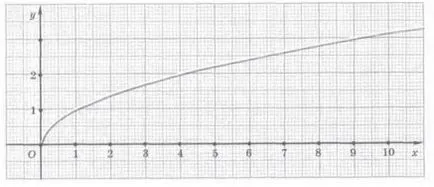
Ábrázolási lehetővé teszi számunkra olyan néhány tulajdonságát az y = x 1/2.
Amikor x = 0, megkapjuk y = 0; x> 0, van y> 0; grafikon átmegy a származási a többi pont a grafikon található, az első koordináta negyedévben.
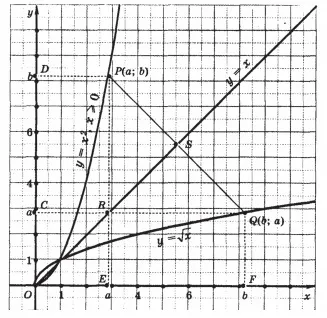
Bizonyítás. A grafikon a függvény az y = x 2, ahol x> 0, egy parabola ága, található az első koordináta negyede. Hagyja, hogy a P pont (a; b) - tetszőleges pontja a grafikonon. Ezután valódi egyenlőség és b = 2. Mivel a feltétellel, hogy nem negatív szám, akkor az is igaz egyenlőség a = b 1/2. Ez azt jelenti, hogy a koordinátákat a Q pont (b, a) átalakítjuk a képlet y = x 1/2 in valódi egyenlőség, vagy más módon, a Q pont (b, a) tartozik a függvény grafikonját y = x 1/2.
Az is bebizonyosodott, hogy ha az M pont (c, d) tartozik a függvény grafikonját y = x 1/2. az a pont N (d; k) tartozik a grafikon y = x 2, ahol x> 0.
Kiderült, hogy minden egyes P pont (a; b) a grafikon y = x 2, ahol x> 0, megfelel az egyedi pont Q (b, a) a függvény grafikonját y = x 1/2, és fordítva.
Továbbra is bizonyítani, hogy a P pont (a; b) és Q (b, a) szimmetrikus a y = x. Feszültségcsökkentő merőlegesek a koordinátatengelyeken a P pontok és Q kapjunk ezen tengelyek E pont (a; 0), D (0; b), F (b; 0) C (0, a). R pontja metszéspontja merőlegesek és PE QC a koordinátái (a, a), és ezért tartozik a y = x. PRQ egy egyenlő szárú háromszög, mert annak oldalai RP és RQ │ b - és az egyes │. Y = x egyenes vonal metszi a szöget, mint a DOF. és PRQ szög és metszi a szegmens PQ, hogy egy bizonyos ponton S. Ezért, az RS szegmens metszi PRQ háromszög. Mivel a felezővonal egy egyenlő szárú háromszög magassága, valamint a középső, a PQ ┴RS és PS = QS. Ez azt jelenti, hogy a P pont (a; b) és Q (b, a) szimmetrikus a y = x.
Mivel a függvény grafikonját y = x 1/2 szimmetrikus grafikákat függvény az y = x 2, ahol x> 0, a vonalhoz képest y = x. majd a grafikon y = x 1/2 egyik ága a parabola.