Hogyan számoljuk ki a kerülete a háromszög

A kerülete bármilyen geometriai formák, beleértve a háromszögek, egyenlő a teljes hossza a határai ez a szám. Ez jelöli latin nagybetű P és könnyen megtalálható hozzáadásával hosszának minden oldalról az ábra.

Szponzor elhelyezés PG Kapcsolódó cikkek „Hogyan kell kiszámítani a kerülete a háromszög” Hogyan találjuk meg a felületét a piramis Hogyan megtalálni a kerülete egy téglalap Hogyan lehet megtalálni a kerülete a háromszög koordinátái által meghatározott a csúcsok

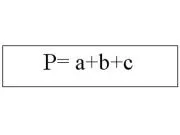
Ahhoz, hogy megtalálja a kerülete olyan háromszög, elegendő megállapítani hossza három oldalán. Egy vegyület Ez a következő: P = a + b + c. Például, ha kapnak ABC háromszög oldalai 5, 8 és 11 cm-es, annak kerülete egyenlő lesz AB + BC + CA = 5 + 8 + 11 = 24 cm.

Ha nem tudja a oldalhossza, de azzal a feltétellel adott háromszög területét, és a kör sugara írva benne, akkor is képes lesz megtalálni a kerület. Ehhez meg kell használni egy háromszög területén képlet: S = r x p, ahol r - a sugara a beírt kör és a p - ez semiperimeter. Semiperimeter megtalálható elosztják a terület sugara (p = S. r), majd szorozzuk meg az eredményt két, hogy teljes kerülete (P = 2p).

Ha a háromszög akkor jobbra, majd megtalálja a kerülete elegendő tudni, csak a hossza a háromból két oldala van. hossz harmadik fél, könnyen megtalálja a Pitagorasz-tétel. Így, ha tudjuk, a hossza két lába (a és b), a kerülete a képlet a következő lesz: P = a + b + V (a2 + b2). Ha tudja, hogy a hossza az egyik lábát (a) és az átfogó (c), akkor a képlet a következőképpen alakul: a + v (c2 - a2) + c.

Továbbá, egy téglalap alakú háromszög területe megtalálható, ha tudod, hogy a hossza mindössze az egyik fél, és az értéke az egyik hegyes szögek. (?) Ha tudja a hossza az egyik lábát (a), és a néző szög, a kerülete megtalálható a következő képlet szerint: P = a x (1. TG + 1. sin + 1 ..). (?) Ha ismert befogó (a), és a bezárt szög, a kerülete a képlet a következő alakú: P = a x (1. CTG + 1. cos + 1 ..). Ha ismeri a átfogója (c) bármely hegyesszögek (. Például), majd a kerülete a területen könnyen megtalálja a képlet: P = (1 + sin + cos.?) X s.