húr rezgés
Cél: tanulmány hullámjelenségek, a létfeltételek állóhullámok, a tanulmány a rugalmas tulajdonságait a húr.
A fő elméleti pozíció
Hagyja pont rezgésbe, ez található olyan környezetben, ahol minden részecske vannak összekötve. Ezután a rezgési energia átvihető pont körül a pontokat, kiváltó azok hinták. A jelenség terjedésének rezgések közegben úgynevezett hullám. Ebben a rezgő részecskék nem mozog a mindent átható rezgési folyamatot, és a körül ingadozik az egyensúlyi helyzetben.
Ha szabadon terjeszthető egyetlen hullám egy végtelen közegben, ez az úgynevezett egy taposómalom. Alkotunk az egyenlet egy haladó hullám, amely lehetővé teszi, hogy meghatározza az elmozdulás bármely pontján a hullámok bármikor.
Ábra. 9.1. Levezetni az egyenletet egy utazó hullám
Tekintsünk egy folytonos homogén közeget
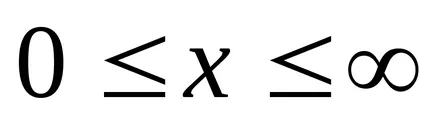

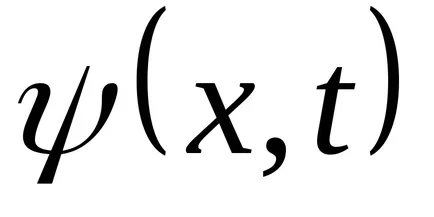
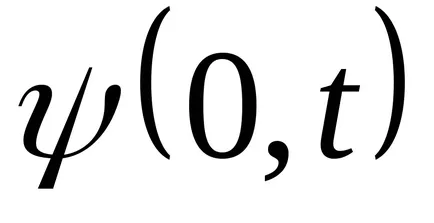


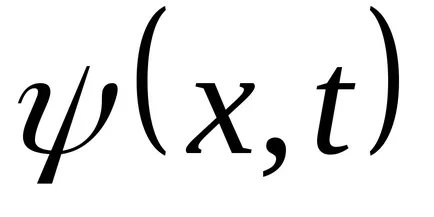
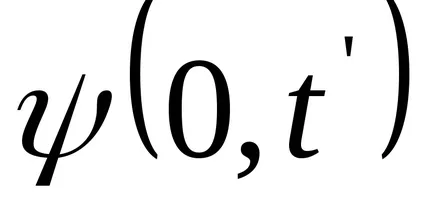


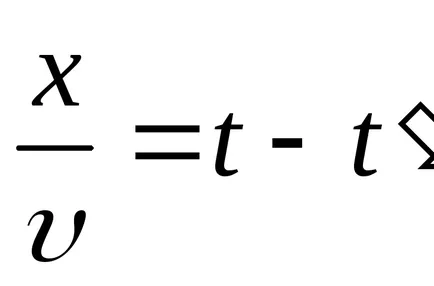
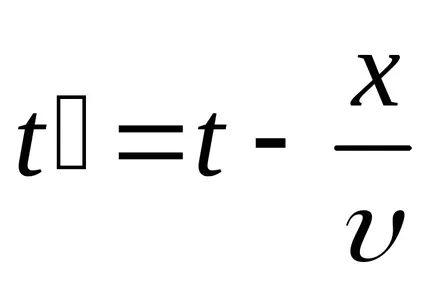
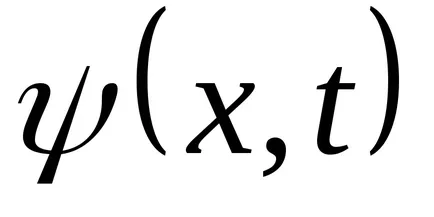
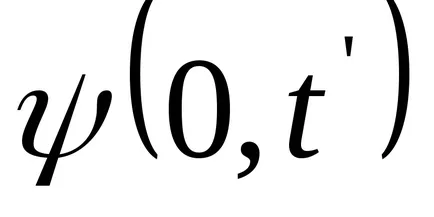

Transform funkció (9.1):
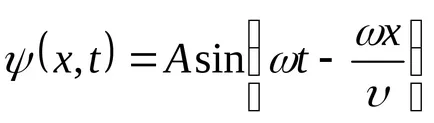
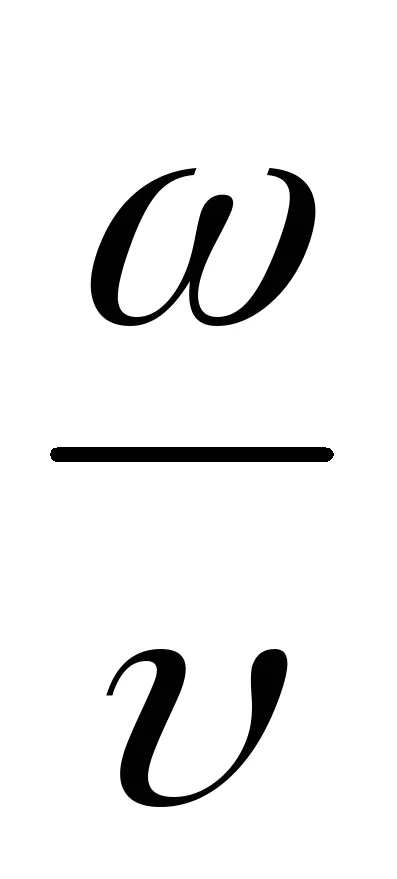
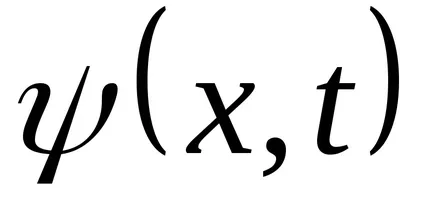
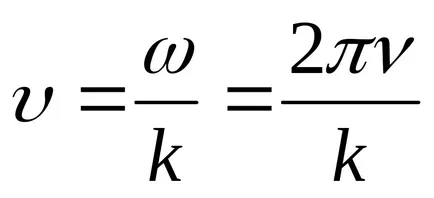


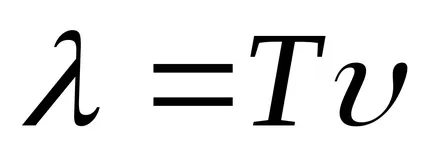
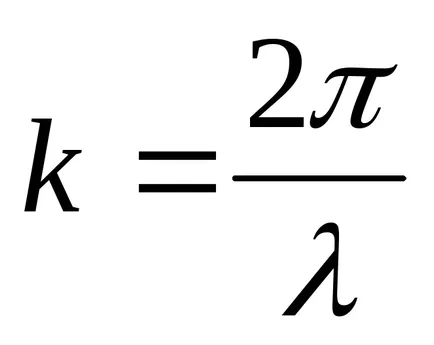
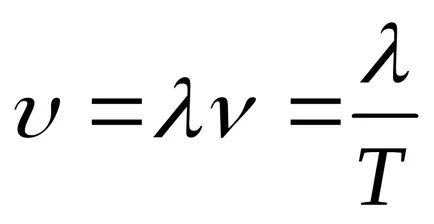
Egyenlet (9.1) az egyenlete az utazó-dimenziós (vagy sík) hullámok. Egy adott x az, hogy meghatározza a helyzetét a pont (ok egyensúlyi helyzet koordináta x) bármely adott időpontban t. Egy adott t lehetővé teszi, hogy meghatározza a pillanatnyi helyzet az oszcilláló pontokat.
Így azt látjuk, hogy a hullámmozgás tart kettős frekvencia. Egyrészt, az egyes részecskék a közeg megy periodikus mozgást idővel, másrészt, az egyes időpontokban, az összes részecskék kerülnek a vonalon, amely alakját periodikusan megismétlődik a térben.
Definiáljuk a terjedési sebessége a longitudinális rezgések mentén démon-során egy hosszú rúd egy állandó keresztmetszetű.
Ábra. 9.2. Szaporítása rugalmas deformáció mentén a rúd
rideystvii a baloldali részen az erő

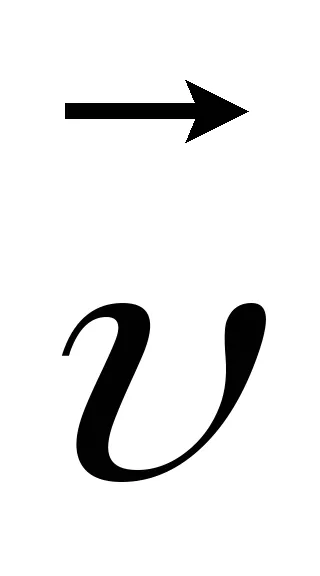
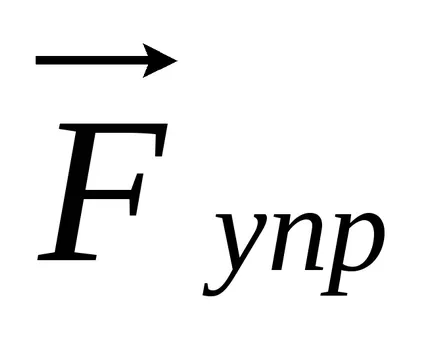
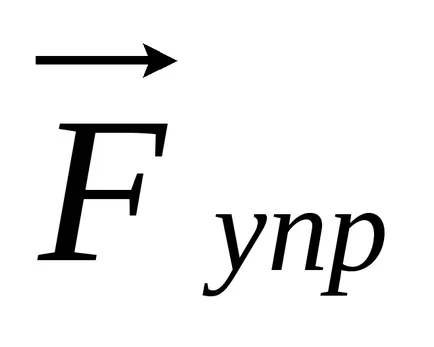

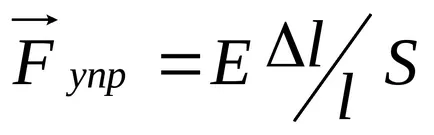

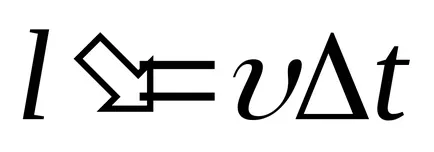
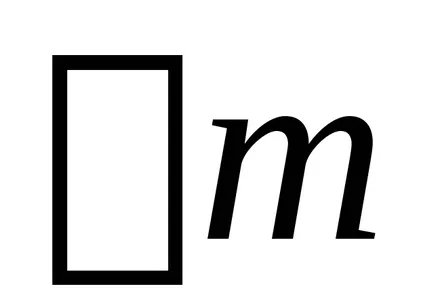
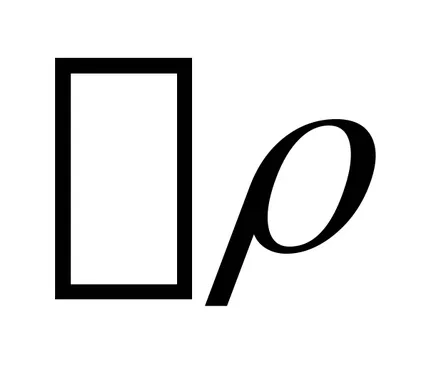
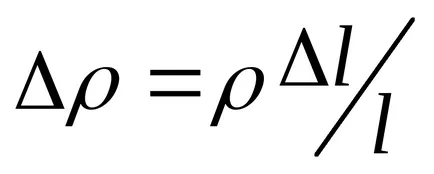
ahol
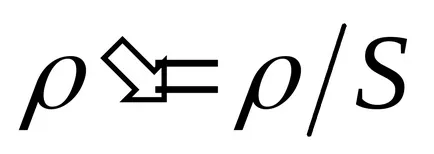
Egyenlet (9.1) egy olyan hullám terjesztő pozitív irányban a tengelye Mr. Oh. Ha megváltoztatja az irányt a hullám terjedési az ellenkező második kifejezés az érv a koszinusz változik jel, mivel

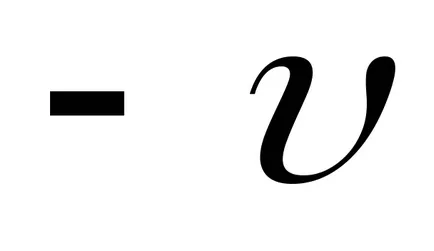
Tekintsük most az terjedése a karakterlánc fix mindkét végén. Ebben a hullám, mozgó egy irányba, miután elérte a második rögzített vége a húr, és szétterül tükröződik az ellenkező irányba. Így hosszában a string hullámok keletkeznek overlay jelenség szaporító ellentétes irányban. Ha a folyadék tulajdonságai nem változnak hatása alatt a szaporítóanyag hullám, a szuperpozíció elve alapján végezzük, ahol minden egyes hullám szaporított a közegben a többitől függetlenül. Ebben az esetben a kapott elmozdulása z közepes részecskék úgy definiáljuk, mint az elmozdulás nagyságát a Z1 és Z2. okozta a folyosón az egyes hullámok. Ennek eredményeként, akkor előfordulhatnak különböző pontjain közepes teljesítményű vagy csillapítása rezgések függő jön perturbáció fázisban.
Addition hullámok, ahol különböző pontjain a közeg vannak kialakítva amplifikáció és csillapítása rezgési amplitúdójának neve interferencia hullámok. Ez az interferencia mintázat tartani.
Tekintsük az interferenciát a két hullám azonos amplitúdójú utazik ellentétes irányban, mint abban az esetben egy string rögzített mindkét végén. Meg kell figyelembe venni a következő jelenség. Visszaverődés után a rögzített végét tükrözi deformáció ellenkező előjellel. Ez érthető, ha figyelembe vesszük, hogy a elmozdulása rögzített vég minden alkalommal hiányzik a rögzítési pont a szemben álló erők a soron következő szövegre hajlítás. Ezek az erők létrehozásához hajlítási ellenkező előjelű, kezd terjedni az ellenkező irányba. Ezért deformáció visszavert torzítás előjel. Ha a visszavert hullám harmonikus ilyen változás felér „veszteség” fél-hullám után gondolkodás.
Így a szuperpozíció két hullám meghozta a következő:
.
A különbség a szinusz képlet, megkapjuk
Ez a kifejezés az úgynevezett állóhullám-egyenlet, feltételezve álló rezgések, azaz a módot, amely akkor fordul elő ismételt hullámok között futnak a húr kötések. Tól (9.4) azt látjuk, hogy az állóhullám környezet minden pontján (x értéknél) szinuszosan változik szögsebességgel .
A rezgési amplitúdó eltérő a különböző pontok és határozza meg (9,4) a következő:
Az utóbbi expressziós következik, hogy van egy olyan pont a közeg, az úgynevezett csomópontok, ahol nem tapasztalhatók hullámzások Zm = 0, így a, z = 0. A koordinátáit ezek a pontok határozzák meg a feltétellel, hogy a sinus (9,5), azaz
Ennélfogva, mivel a
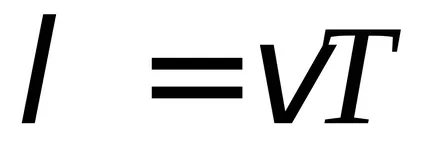
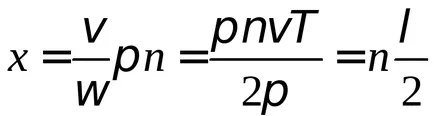
Ezért, a távolság a szomszédos csomópontok felével egyenlő a hullámhossz. Mivel csomópontok mindenkor marad nyugalomban, az állóhullám nem irányul energia transzfer, az energia nem tud átjutni a csomóponton. Az energia átvitelét mentén a húr csak egy mozgó hullám.
Azok a pontok, ahol az amplitúdó értéke eléri a maximális

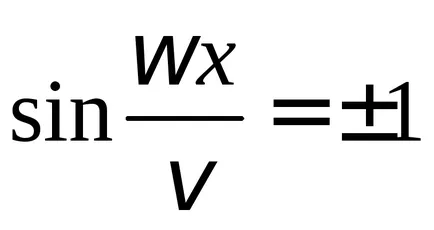
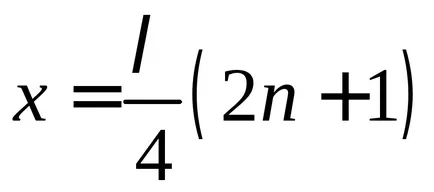
tényező
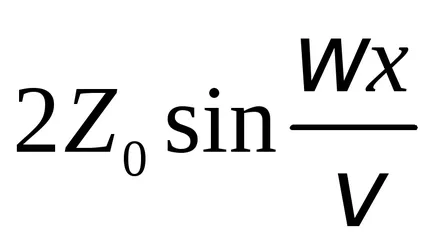
Ily módon egy álló hullám keletkezik csak akkor, ha megfelelő arányban string size és hullámhossz (oszcillációs frekvencia). Különböző értékei n = 1, 2, ... megkapjuk különböző típusú vagy módok rezgések, ahol n számát határozza meg amplitúdópontok és csomópontok nem. Tól (9.6) és (9.7) megkapjuk a kifejezés a frekvenciák, amelyeken az álló hullámok jönnek létre a húr
frekvenciák
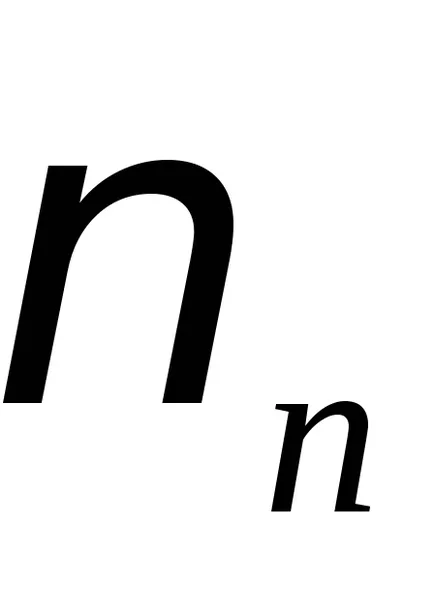
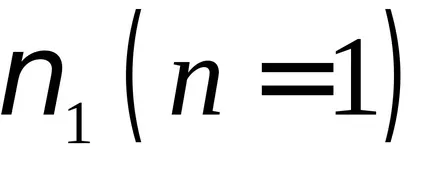
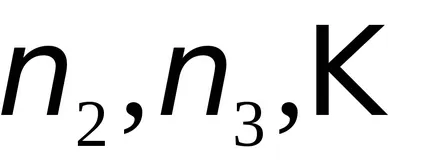
Általánosságban elmondható, hogy a húr rezgések létezhet más természetes frekvenciákat. Így, együtt az alapvető hang n = 1, lehet izgatott felhangokkal n = 2, 3, 4, ....
Fentebb kapott egyenletek írják le a mozgás tökéletesen rugalmas karakterlánc vákuumban. Amikor a rezgések a szöveg mindig egy igazi energia veszteség adódik.
Része az energia vész el a levegő súrlódás, a másik része átmegy a végén a húr, stb Ahhoz, hogy csillapítatlan rezgések egy vibrátor. Ha az energia veszteség a pontosság kompenzálja az érkező energia vibrátor, a húr látható állóhullámok. De most, a húr kell az energia átvitelét. Ezért utazó hullámok léteznek együtt állva, aminek következtében egyes oldalak elmosódott lesz. Ha az energia veszteséget időszakra képest csekély a kínálat rezgési energiát a húr, a torzítás a haladó hullámú állóhullám jelentéktelen lesz.
Egy másik megközelítés, hogy a fenti elmélet elhanyagolása húr heterogenitás. A valós húrok és sűrűsége, és a feszültség lehet folytonos függvények koordinátáinak X. Például, ha a húr függőlegesen felfüggesztett, a súlya a húr számla vezet az a tény, hogy a feszültség a felső részek nagyobb, mint az alsó. Bármilyen inhomogenitás torzulásához vezethet a hullámforma, hiszen a szinuszrezgéssel a tér csak egy jellemző normál módok homogén rendszereket.