Inhomogén lineáris differenciálegyenletek véletlenszerű együtthatók
Tekintsük az egyenlet formájában
A jelöléssel írhatunk:
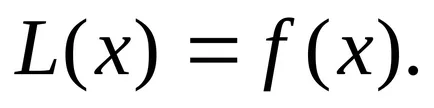
Ebben az esetben feltételezzük, hogy az együtthatók és a jobb oldalon az egyenlet folytonos bizonyos intervallumban (véges vagy végtelen).
Teorema.Obschee oldatot az inhomogén lineáris differenciálegyenlet egy régióban az összege valamennyi döntések és az általános megoldás a megfelelő homogén lineáris differenciálegyenlet.
Bizonyítás. Legyen Y - a megoldás az inhomogén egyenlet.
Akkor helyettesítésével ez a megoldás az eredeti egyenlet kapjuk az identitás:
enged
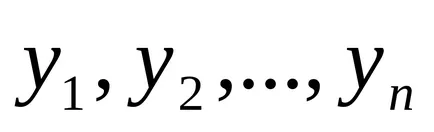
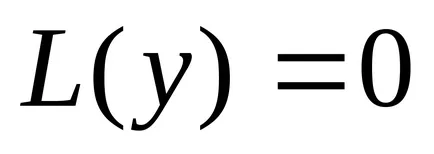
Megmutatjuk, hogy az összeg az általános megoldás az inhomogén egyenlet.

Általánosságban elmondható, Y oldatot lehet beszerezni az általános megoldás, mert Ez egy különleges megoldás.
Így, összhangban ez a tétel, hogy megoldja a lineáris inhomogén differenciálegyenlet meg kell találnunk egy általános megoldást a megfelelő homogén egyenletek és valamilyen módon, hogy megtalálja egy adott megoldást az inhomogén egyenlet. Általában ez a kiválasztás.
Ez kényelmes használni a módszert variációs tetszőleges állandók.
Ehhez először megtalálni az általános megoldás a megfelelő homogén egyenlet formájában:
Ezután feltéve koeffitsientyCifunktsiyami szort, azt keresik a megoldást az inhomogén egyenlet:
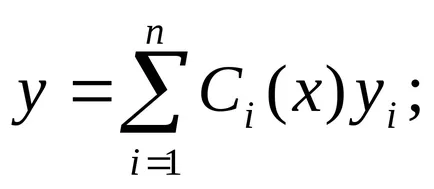
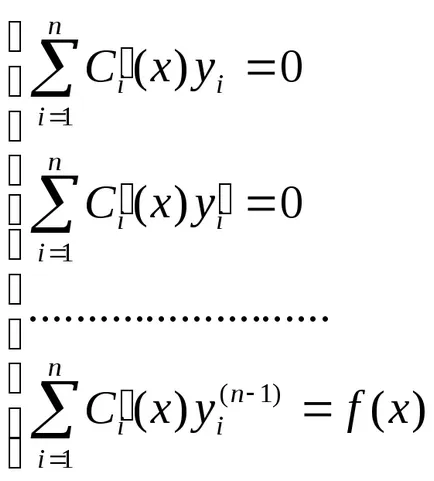
Példa. egyenlet megoldásához
Megoldása homogén lineáris egyenlet
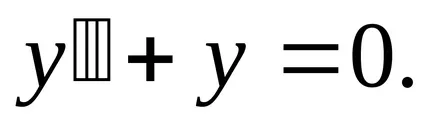
A megoldás az inhomogén egyenlet fog kinézni:
Minősül egyenletrendszert:
Mi megoldjuk ezt a rendszert:
A kapcsolat találják funktsiyuA (x).
Most azt látjuk, a B (x).
Helyettesítse a kapott értékek az általános megoldás az inhomogén egyenlet képlet:
Így lehetséges volt, hogy ne találjanak egy adott megoldás az inhomogén egyenlet próbálgatással.
Általánosságban, a módszer a variációs tetszőleges állandók alkalmas megoldásokat találjunk bármely lineáris inhomogén egyenlet. de mivel megtalálása az alapvető rendszer megoldások a megfelelő homogén egyenlet lehet elég nagy kihívás, ez a módszer elsősorban alkalmazott nem homogén egyenletek állandó együtthatós.
Inhomogén lineáris differenciálegyenletek állandó
Az egyenlet jobb oldalán egy speciális fajtája.
Ez elképzelhető formában egy adott megoldás típusától függően a jobb oldalon az inhomogén egyenlet.
Vannak az alábbi esetekben:
I. A jobb oldalon a inhomogén lineáris differenciálegyenlet a formája:
ahol - polinom stepenim.
Ezután egy bizonyos oldatot kérik formájában:
Itt, Q (X) - a polinom ugyanolyan mértékben, mint a P (x). de meghatározatlan együtthatók, és r - egy szám jelzi, hogy hány alkalommal száma gyöke a karakterisztikus egyenlet a megfelelő homogén lineáris differenciálegyenlet.
Példa. egyenlet megoldásához
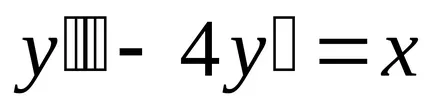
Mi megoldjuk a megfelelő homogén egyenlet:
Most azt látjuk, egy adott megoldás az eredeti inhomogén egyenlet.
Vessük össze a jobbra mutató jobb oldali, a fent tárgyalt.
A különösen oldatot kérik formájában, ahol a
Most határozzuk meg az ismeretlen együtthatók A és B
Behelyettesítve egy adott oldat általános formája a kezdeti inhomogén differenciálegyenlet.
Összesen részleges megoldást:
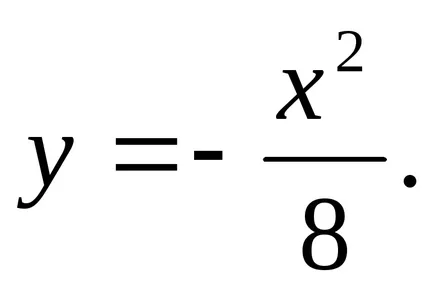
Ezután az általános megoldás az inhomogén lineáris differenciálegyenlet:
II. A jobb oldalon a inhomogén lineáris differenciálegyenlet a formája:
Aztán egy partikuláris megoldása az inhomogén egyenlet fog kinézni:
ahol a számos r mutatja, hogy hányszor száma
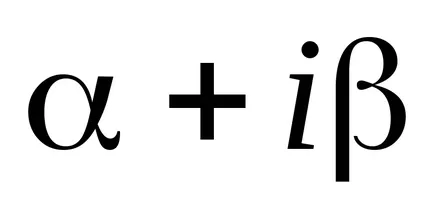
Megjegyezzük, hogy ha a jobb oldalon az egyenlet kombinációja kifejezések a fentiekben tárgyalt, a megoldás kombinációja megoldások a kiegészítő egyenletek, amelyek mindegyike a jobb oldalon expressziójának megfelelő a kombináció.
Ie Ha az egyenlet a formában, majd egy adott megoldást ennek az egyenletnek
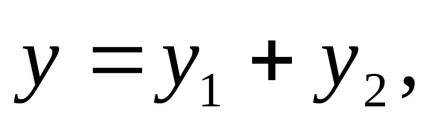
Annak illusztrálására példaként megoldására egy másik módszer a fentiekben tárgyaltuk.
Példa. egyenlet megoldásához
Összetétele és megoldani a karakterisztikus egyenlet: