iteratív módszerek
A nagy ismeretlenek száma a lineáris egyenletrendszer Gauss-elimináció rendszer, amely a pontos megoldás, akkor elég nehéz. Ebben az esetben, hogy megtalálják a gyökerek könnyebben használható közelítő iteratív módszereket. Tekintsük az iterációs módszer (Seidel-módszer).
Adott egy rendszer
Feltételezve, hogy az átlós feltételeket - az együtthatók nem nulla


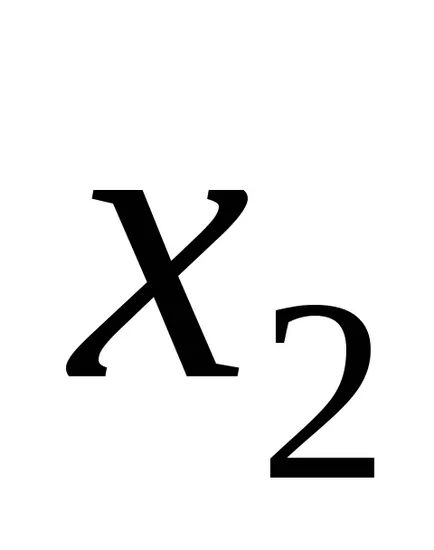
A rendszer (2) úgy érik el egymást követő közelítések. Mivel a nulla közelítés bármilyen értéket felvehet. Gyakran használjuk ezt a oszlopon szabad feltételeket.

A következő közelítés úgy számítjuk ki, hogy ebben az esetben az értékeket
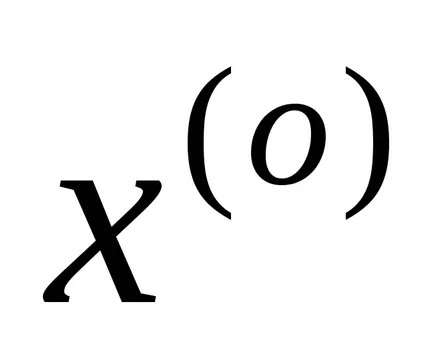
,
második közelítése számítják át az első:
.
Ha a szekvenciája közelítések


ez a határérték egy olyan megoldás a (2), és ennek következtében, a rendszer (1).
Írunk képlet közelítő kibővített formában:
A módszer az egymást követő közelítések, képlettel definiált (3) nevezzük iterációval. Az iteratív folyamat konvergál is, azaz a számú közelítések megszerzéséhez szükséges a gyökérzet (1) egy adott pontossággal kicsi, ha a mátrix elemeinek

Tekintsük a rendszer lineáris algebrai egyenletek három ismeretlennel:
Kiválasztjuk a jobb oldalon minden egyenlet átlós ismeretlen
A nulla (kezdeti) megközelítés a problémák néhány érték úgy döntünk, az ismeretlen, és hagyja, hogy

A rendszer (3) kiszámításához az ismeretlen


Általában, hogy iteráció k- rendszer úgy néz ki, mint ez:
Azaz, az aktuális érték az ismeretlen azonnal használható a későbbi számításokban. Ezt a módszert nevezik iteratív módszer Gauss - Seidel.


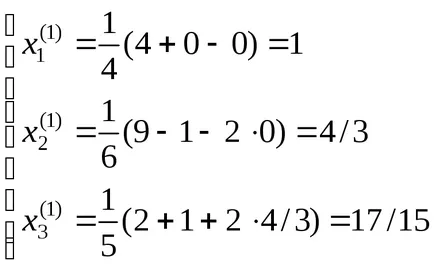
Egzakt megoldás által kért iteratív folyamat () fogadja a 5-6-edik iteráció.
Abban az esetben, egy rendszer n egyenletek k - th közelítés a megoldás az lenne,:
Az iteratív folyamat addig folytatódik, amíg az összes

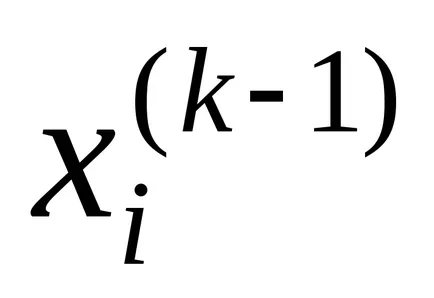
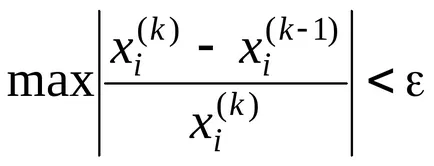
Tekintsük a módszer konvergencia kérdéseket. Adott egy rendszer két egyenlet
,
Tól (1) és (3) megkapjuk
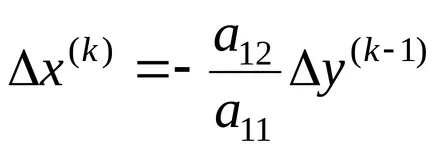

Az utolsó egyenlet a következő:
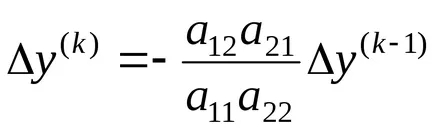
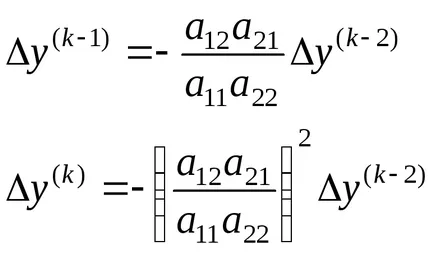
Folytatva, akkor kap:

Ebből következik, hogy az iteratív folyamat Gauss - Seidel
konvergens, ha a megközelítés, hogy a k iterációs lesz jelentősen eltér az első közelítés. Ez csak akkor lehetséges, azzal a feltétellel:

ami azt jelenti, hogy az átlós tagok elsőbbséget élveznek a többiekkel.
A módszer előnye az eliminációs hogy véges és elméletileg fel lehet használni, hogy megoldja minden nem degenerált rendszer lineáris algebrai egyenletek. Iteratív Gauss-Seidel módszer konvergál csak különleges egyenletrendszerek. Azonban, ha az iterációs módszer konvergál, akkor előnyös:
számítási idő
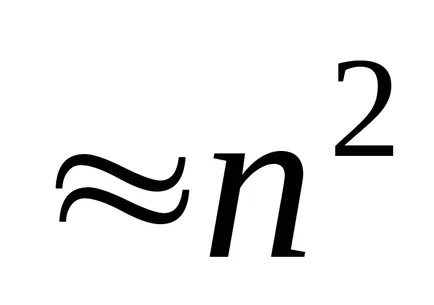

kerekítési hiba iteratív módszer kevesebb.
nagy rendszerek egyenletek nem lehet pontosan megoldható közvetlen módszerek.